Trắc nghiệm Hàm số mũ. Hàm số lôgarit Toán Lớp 12

Câu 1:

Nam định mua một chiếc xe máy theo phương thức trả góp. Theo phương thức này sau một tháng kể từ khi nhận xe phải trả đều đặn mỗi tháng một lượng tiền nhất định nào đó, liên tiếp trong vòng 24 tháng. Giả sử giá xe máy thời điểm Nam mua là 16 triệu (đồng) và giả sử lãi suất công ty tài chính cho vay tiền  là 1% một tháng trên số tiền chưa trả. Với mức phải trả hàng tháng gần với kết quả nào sau đây nhất thì việc mua trả góp là chấp nhận được ?

Câu 2:

Cường độ một trận động đất M được cho bởi công thức \(M=\log A-\log {{A}_{0}}\), với A là biên độ rung chấn tối đa và \({{A}_{0}}\) là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, trận động đất khác ở gần đó đo được 7,1 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu trận động đất này.

Câu 3:

Biết rằng năm 2001, dân số Việt Nam là 78.685.800 người và tỉ lệ tăng dân số năm đó là 1,7%. Cho biết sự tăng dân số được ước tính theo công thức \(S=A.{{e}^{Nr}}\) (trong đó A: là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người.

Câu 4:

Một người gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi kép (sau 3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng, người đó gửi thêm 50 triệu đồng với kì hạn và lãi suất như trước đó. Cho biết số tiền cả gốc và lãi được tính theo công thức \(T=A{{(1+r)}^{n}}\), trong đó A là số tiền gửi, r là lãi suất và n là số kì hạn gửi. Tính tổng số tiền người đó nhận được 1 năm sau khi gửi tiền.

Câu 5:

Một sinh viên được gia đình gửi tiết kiệm số tiền vào ngân hàng với số tiền là 20 triệu đồng theo mức kì hạn 1 tháng với lãi suất tiết kiệm là 0,4%/tháng. Nếu mỗi tháng anh sinh viện rút ra một số tiền như nhau vào ngày ngân hàng tính lãi thì hàng tháng anh ta rút ra bao nhiêu tiền để sau 5 năm, số tiền vừa hết?

Câu 6:

Một người gửi 15 triệu đồng vào ngân hàng theo thể  thức lãi kép kỳ hạn 1 quý với lãi suất 1,65% một quý. Hỏi sau bao lâu người đó có được ít nhất 20 triệu đồng cả vốn lẫn lãi từ số vốn ban đầu?

Câu 7:

Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi đơn, kì hạn 3 tháng với lãi suất 3% một quý. Hỏi người đó phải gửi trong ngân hàng ít nhất bao lâu, số tiền thu về hơn gấp hai số tiền vốn ban đầu?

Câu 8:

Năng lượng giải toả E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởi công thức: \(\log \left( E \right)=11,4+1,5M\). Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải toả tại tâm địa chấn của nó gấp 14 lần trận động đất ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu? ( kết quả làm tròn đến hàng phần trục)

Câu 9:

Peter dùng 80 mg thuốc để điều chỉnh huyết áp của mình. Đồ thị dưới đây là đồ thị của hàm số mũ có dạng ( với x thời gian (ngày) sau khi tiêm thuốc, r tỉ lệ về lượng thuốc của ngày hôm trước còn lại hoạt động trong máu của Peter , y lượng thuốc còn tác dụng sau x ngày tiêm thuốc), chỉ số lượng thuốc đầu tiên và số lượng thuốc còn lại hoạt động trong máu của Peter sau một, hai, ba và bốn ngày.

Hình minh hoạ:  Lượng thuốc còn theo ngày

Lượng thuốc còn lại là bao nhiêu vào cuối ngày thứ nhất?

Câu 10:

Theo thể thức lãi kép, nghĩa là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp. Nếu một người gửi số tiền A với lãi suất r mỗi kì thì sau N kì, số tiền người ấy thu được cả vốn lẫn lãi là \(C=A{{\left( 1+r \right)}^{N}}\) (triệu đồng). Nếu bạn gửi 20 triệu đồng vào ngân hàng X theo thể thức lãi kép với lãi suất 8,65% một quý thì sau 3 năm (vẫn tính lãi suất kì hạn theo quý), bạn sẽ thu được số tiền cả vốn lẫn lãi gần với giá trị nào nhất sau đây (giả sử lãi suất hằng năm của ngân hàng X là không đổi) ?

Câu 11:

Tỷ lệ tăng dân số hàng năm của Việt Nam là 1,07%. Năm 2016, dân số của Việt Nam là 93422000 người. Hỏi với tỷ lệ tăng dân số như vậy thì năm 2026 dân số Việt Nam gần với kết quả nào nhất?

Câu 12:

Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quí), lãi suất 6% một quí theo hình thức lãi kép ( lãi cộng với vốn). Sau đúng 6 tháng, người đó lại gửi thêm 100 triệu đồng với hình thức và lãi suất như trên. Hỏi sau 1 năm tính từ lần gửi đầu tiên người đó nhận số tiền gần với kết quả nào nhất?

Câu 13:

Thang đo Richter được Charles Francis Richter đề xuất và sử dụng lần đầu tiên vào năm 1935 để sắp xếp các số đo độ chấn động của các cơn động đất với đơn vị là độ Richter. Công thức tính độ chấn động như sau: \({{M}_{L}}=\log A-\log {{A}_{o}}\), với \({{M}_{L}}\) là độ chấn động, A là biên độ tối đa đo được bằng địa chấn kế và \({{A}_{o}}\) là một biên độ chuẩn. (nguồn: Trung tâm tư liệu khí tượng thủy văn). Hỏi theo thang độ Richter, với cùng một biên độ chuẩn thì biên độ tối đa của một trận động đất 7 độ Richter sẽ lớn gấp mấy lần biên độ tối đa của một trận động đất 5 độ Richter ?

Câu 14:

Biểu đồ bên cho thấy kết quả thống kê sự tăng trưởng về số lượng của một đàn vi khuẩn : cứ sau 12 tiếng thì số lượng của một đàn vi khuẩn tăng lên gấp 2 lần. Số lượng vi khuẩn ban đầu của đàn là 250 con. Công thức nào dưới đây thể hiện sự tăng trưởng về số lượng của đàn vi khuẩn N tại thời điểm t ?

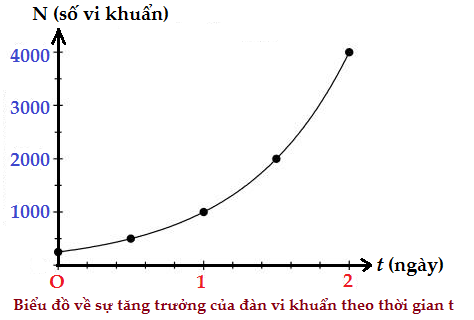
Câu 15:

Cường độ một trận động đất M (richter) được cho bởi công thức \(M=\log A-\log {{A}_{0}}\), với A là biên độ rung chấn tối đa và \({{A}_{0}}\) là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ gần với số nào sau đây nhất là:

Câu 16:

Sự tăng trưởng của một loại vi khuẩn tuân theo công thức \(S=A.{{e}^{rt}}\), trong đó A là số lượng vi khuẩn ban đầu,r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để  số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng t gần với kết quả nào sau đây nhất.

Câu 17:

Năm 1994, tỉ lệ thể tích khí \(C{{O}_{2}}\) trong không khí là \(\frac{358}{{{10}^{6}}}\). Biết rằng tỉ lệ thể tích khí \(C{{O}_{2}}\) trong không khí tăng 0,4% hàng năm. Hỏi năm 2004, tỉ lệ khí \(C{{O}_{2}}\) trong không khí gần với số nào sau đây nhất?

Câu 18:

Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bằng công thức : \(m\left( t \right)={{m}_{o}}{{\left( \frac{1}{2} \right)}^{\frac{t}{T}}}\) trong đó \({{m}_{0}}\) là khối lượng chất phóng xạ ban đầu ( tại thời điểm t=0), \(m\left( t \right)\) là khối lượng chất phóng xạ tại thời điểm t, T là chu kì bán rã ( tức là khoảng thời gian để một nửa số nguyên tử của chất phóng xạ bị biến thành chất khác).

Cho biết chu kì bán rã của một chất phóng xạ là 24 giờ (1 ngày đêm). Hỏi 250gam chất đó sẽ còn lại bao nhiêu sau 3,5 ngày đêm ? (Kết quả làm tròn đến 3 chữ số thập phân sau dấu phẩy)

Câu 19:

Một khu rừng có trữ lượng gỗ \({4.10^5}\) mét khối. Biết tốc độ sinh trưởng của các  cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ ?

Câu 20:

Áp suất không khí P (đo bằng milimet thuỷ ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x (đo bằng mét), tức P giảm theo công thức \(P={{P}_{0}}{{e}^{xi}}\) trong đó \({{P}_{0}}=760mmHg\) là áp suất ở mực nước biển \(\left( x=0 \right)\), i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí là 672,71mmHg. Hỏi áp suất không khí ở độ cao 3000m gần với số nào sau đây nhất?

Câu 21:

Nếu cường độ âm tăng lên 1000 lần thì độ to của âm thay đổi như thế nào?

Câu 22:

Tỉ lệ tăng dân số hàng năm của Ấn độ là 1,7%. Năm 1998, dân số của Ấn độ là 984 triệu. Hỏi sau bao nhiêu năm dân số của Ấn độ sẽ đạt 1,5 tỉ? ( Kết quả là tròn đến hàng đơn vị)

Câu 23:

Tỉ lệ tăng dân số hàng năm của Nhật là 0,2%. Năm 1998, dân số của Nhật là 125932000. Vào năm nào dân số của Nhật sẽ là 140000000 ? ( Kết quả làm tròn đến hàng đơn vị)

Câu 24:

Biết rằng tỉ lệ giảm dân hàng năm của I – ta – li -a là 0,1%. Năm 1998, dân số  của Nga là 56783000 người. Hỏi năm 2020 dân số của nước này gần với số nào sau đây nhất?

Câu 25:

Biết rằng tỉ lệ giảm dân hàng năm của Nga là 0,5%. Năm 1998, dân số  của Nga là 146861000 người. Hỏi năm 2008 dân số của Nga gần với số nào sau đây nhất?

Câu 26:

Tỉ lệ tăng dân số hàng năm của In – đô – nê – xia – a là 1,5%. Năm 1998, dân số của nước này là 212942000 người. Hỏi dần số của In – đô – nê – xia – a vào năm 2006 gần với số nào sau đây nhất?

Câu 27:

Bố Hùng để dành cho Hùng 11000 USD để học đại học trong ngân hàng theo hình thức lãi kép với lãi suất 0,73% một tháng. Mỗi tháng Hùng đến rút 60USD để sinh sống. Nếu mỗi tháng rút 200 USD thì sau bao lâu sẽ hết tiền? ( Kết quả làm tròn đến hàng đơn vị)

Câu 28:

Bố Hùng để dành cho Hùng 11000 USD để học đại học trong ngân hàng theo hình thức lãi kép với lãi suất 0,73% một tháng. Mỗi tháng Hùng đến rút 60USD để sinh sống. Hỏi sau một năm số tiền còn lại là bao nhiêu? ( Kết quả làm tròn đến hàng đơn vị)

Câu 29:

Lãi suất của tiền gửi tiết kiệm của một ngân hàng thời gian qua liên tục thay đổi. Bạn Hùng gửi số tiền ban đầu là 5 triệu đồng với lãi suất 0,7% tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,15% tháng trong  nửa năm tiếp theo và bạn Hùng tiếp tục gửi. Sau nửa năm đó lãi suất giảm xuống còn 0,9% tháng. Bạn Hùng tiếp tục gửi thêm một số tháng tròn nữa. Biết rằng khi rút ra số tiền bạn Hùng nhận được cả vốn lẫn lãi là 5747478,359 đồng (chưa làm tròn). Hỏi bạn Hùng đã gửi tiết kiệm trong bao nhiêu tháng ? (Trong suốt quá trình gửi thì lãi nhập gốc)

Câu 30:

Một học sinh 16 tuổi được hưởng tài sản thừa kế 200 000 000 VNĐ. Số tiền này được bảo quản trong một ngân hàng với kì hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền này khi đã đủ 18 tuổi. Biết rằng khi đủ 18 tuổi, số tiền mà học sinh này được nhận sẽ là 228 980 000 VNĐ. Vậy lãi suất kì hạn 1 năm của ngân hàng này là bao nhiêu ?

Câu 31:

Câu 1:Một người gửi tiết kiệm theo ngân hàng một số tiền là 500 triệu đồng, có kì hạn 3 tháng (sau 3 tháng mới được rút tiền), lại suất 5,2% một năm, lãi nhập gốc (sau 3 tháng người đó không rút tiền ra thì tiền lãi sẽ nhập vào gốc ban đầu). Để có số tiền ít nhất là 561 triệu động thì người đó phải gửi bao nhiêu tháng ? ( Kết quả làm tròn hàng đơn vị)

Câu 32:

Sau nhiều năm làm việc anh Nam tiết kiệm được P đồng, dự định số tiền đó để mua một căn nhà. Nhưng hiện nay với số tiền đó thì anh ta chưa thể mua được ngôi nhà vì giá trị ngôi nhà mà anh ta muốn mua là 2P đồng. Vì vậy anh Nam gửi tiết kiệm số tiền này vào ngân hàng Sacombank. Theo bạn sau bao nhiêu năm anh Nam mới có thể sở hữu được ngôi nhà đó. Biết rằng lãi suất gởi tiết kiệm là 8,4% một năm , lãi hằng năm được nhập vào vốn và giá của ngôi nhà đó không thay đổi trong 12 năm tới. ( Kết quả làm tròn đến hàng đơn vị)

Câu 33:

Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn một quý với lãi suất 1,65% một quý. Hỏi sau bao nhiêu quý thì người đó có được ít nhất 20 triệu ?

Câu 34:

Cho hai số thực thỏa mãn \(\log _{2} a+\log _{3} b=1\). Giá trị lớn nhất của biểu thức \(P=\sqrt{\log _{3} a}+\sqrt{\log _{2} b}\)

Câu 35:

Xét các số thực a , b thỏa mãn điều kiện \(\frac{1}{3}<b<a<1\). Tim giá trị nhỏ nhất của biểu thức \(P=\log _{a}\left(\frac{3 b-1}{4}\right)+12 \log _{\frac{b}{a}}^{2} a-3\)

Câu 36:

Cho \(x>y \geq 0\) thỏa mãn \(3^{x+y+2 x y-2}=\frac{2(1-x y)}{x+y}\) . Giá trị nhỏ nhất của biểu thức P=x+5 y là:

Câu 37:

Cho \(x>0 ; y>0 \text { và } 2020^{2019\left(x^{2}-y+4\right)}=\frac{4 x+y}{(x+2)^{2}}\) . Tìm giá trị nhỏ nhất của biểu thức \(P=y-2 x ?\)

Câu 38:

Cho a,b,c>1 và các số thực dương x, y, z thỏa mãn \(a^{x}=b^{y}=c^{\frac{a}{2}}=\sqrt{a b c}\) . Tìm giá trị lớn nhất của \(P=\frac{1}{x}+\frac{1}{y}-z^{2}\)

Câu 39:

Cho x, y dương thỏa mãn: \(\log _{3}\left(x^{2}+2 y\right)=1+\log _{3} 4\). Giá trị lớn nhất của \(P=\sqrt{x y}\) thuộc khoảng nào 

Câu 40:

Cho biết a, b, c là các số thực dương thỏa mãn \(2018^{a}=2019^{b}=2020^{c}\) . Hãy tính giá trị của biểu thức \(P=\frac{a}{b}+\frac{b}{c}\)

Câu 41:

Cho \(\mathrm{x}, y, a, b]\) là các số dương thỏa mãn \(a>b>1 \text { và } a^{x+1}=b^{2 y}=\frac{a}{b}\) . Giá trị nhỏ nhất của biểu thức \(P=x^{2}+y^{2}+y\) là:

Câu 42:

Cho hai số thực dương x, y thỏa mãn \(\log _{4} x=\log _{6} y=\log _{9}(x+y) \text { . Giá trị của tỉ số } \frac{x}{y} \text { bằng }\)

Câu 43:

Cho x, y, z là ba số thực khác 0 thỏa mãn \(2^{x}=5^{y}=10^{-z} . \text { Tính } P=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)

Câu 44:

\(\text { Cho } 2^{a}=3,3^{b}=4,4^{c}=5,5^{d}=6 \text { . Tính } 2^{a b c d} \text { . }\)

Câu 45:

Phương trình \(\log (x+1)=2\) có nghiệm là

Câu 46:

Cho x, y là các số thực thỏa mãn \(\log _{2}(2 x+2)+x-3 y=8^{y}(*)\) . Biết \(0 \leq x \leq 2018\),  số cặp x, y nguyên thỏa mãn đẳng thức (*) là 

Câu 47:

Cho \(f(x)=2020^{x}-2020^{-x}\) . Gọi \(m_{0}\) là số lớn nhất trong số nguyên m thỏa \(f(m+1)+f\left(\frac{m}{2020}-2020\right)<0\) . Giá trị của m₀ là 

Câu 48:

Có bao nhiêu cặp số nguyên (x; y) thỏa mãn \(0 \leq x \leq 2020 \text { và } 3\left(9^{y}+2 y\right)=x+\log _{3}(x+1)^{3}-2 ?\)

Câu 49:

Cho hai số thực x y , thỏa mãn \(0 \leq x, y \leq 1\) trong đó x, y không đồng thời bằng 0 hoặc 1 và \(\log _{3}\left(\frac{x+y}{1-x y}\right)+(x+1)(y+1)-2=0\). Tìm giá trị nhỏ nhất của \(P=2 x+y \text { . }\)

Câu 50:

Cho số thực thỏa mãn \(2^{x^{2}}-2^{y}=y-x^{2}\) . Tìm giá trị lớn nhất của biểu thức \(P=x-2 y\)