Trắc nghiệm Khái niệm về thể tích của khối đa diện Toán Lớp 12
-
Câu 1:
Trong các mệnh đề sau, mệnh đề nào ĐÚNG?
-
Câu 2:
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích bằng 2110. Biết A'M = MA; DN = 3ND'D; CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằn
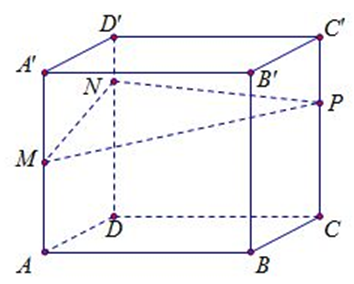
-
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là điểm nằm trên cạnh CD. Tính thể tích khối chóp S.ABM.
-
Câu 4:
Cho hình lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A' lên (ABC) là trung điểm của BC. Tính thể tích V của khối lăng trụ ABC.A'B'C' biết AB = a, AC = \(a\sqrt 3 \), AA' = 2a.
-
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SO tạo với mặt phẳng đáy một góc 450. Tính thể tích V của khối chóp S.ABCD.
-
Câu 6:
Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 3a, BC = a. Cạnh bên SA vuông góc với đáy; SC tạo với mặt phẳng (ABCD) một góc 600. Tính thể tích V của khối chóp đã cho.
-
Câu 7:
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
-
Câu 8:
Cho hình chóp S.ABCD đáy hình chữ nhật, SA vuông góc đáy, AB = a; AD = 2a.AB = a; AD = 2a. Góc giữa SB và đáy bằng 45°. Thể tích khối chóp là.
-
Câu 9:
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật. Tính thể tích S.ABCD biết AB = a; AD = 2a; SA = 3a.
-
Câu 10:
Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần
-
Câu 11:
Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng:
-
Câu 12:
Trong các mệnh đề sau đây, mệnh đề nào đúng?
-
Câu 13:
Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng \(a\sqrt 3 \). Tính thể tích khối chóp A'.ABCD.
-
Câu 14:
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính theo a thể tích V của khối chóp S.ABCD.
-
Câu 15:
Cho khối chóp đều S.ABC có cạnh đáy bằng a. Tính thể tích khối chóp S.ABC biết cạnh bên bằng a.
-
Câu 16:
Cho hình chóp S.ABC có SB vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông cân đỉnh B, cạnh huyền AC = \(a\sqrt 2 \), mặt bên (SAC) hợp với đáy một góc 600. Tính thể tích khối chóp S.ABC.
-
Câu 17:
Cho hình chóp S.ABC có đáy là tam giác vuông tại A; AB = a; AC = 2a. Đỉnh S cách đều A,B,C; mặt bên (SAB) hợp với mặt đáy (ABC) góc 600. Tính thể tích khối chóp S.ABC.
-
Câu 18:
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 300. Tính thể tích của lăng trụ đã cho theo a.
-
Câu 19:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SD = \frac{{\sqrt {13} }}{2}\). Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Thể tích khối chóp S.ABCD là:
-
Câu 20:
Cho hình chóp tam giác S.ABC có \(SA = SB = SC = a\sqrt 2 \), tam giác ABC vuông cân tại A và BC = 2a. Tính thể tích V của khối chóp S.ABC.
-
Câu 21:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt đáy, góc giữa SC và mặt đáy bằng 300. Thể tích khối chóp S.ABC là:
-
Câu 22:
Cho khối chóp S.ABC có SA vuông góc với đáy, SA=4, AB=6, BC=10 và CA=8. Tính thể tích V của khối chóp S.ABC.
-
Câu 23:
Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a và cạnh bên bằng 9a. Tính thể tích khối lăng trụ đó.
-
Câu 24:
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm H của cạnh AB và AA' = \(a\sqrt 2 \). Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
-
Câu 25:
Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và AC = \(a\sqrt 2 \). Tính thể tích V của khối lăng trụ đã cho.
-
Câu 26:
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng \(a\sqrt 3 \). Tính thể tích khối chóp S.ABCD.
-
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
-
Câu 28:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA = AC = 2a. Tính thể tích khối chóp S.ABC.
-
Câu 29:
Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho.
-
Câu 30:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với mặt phẳng (SAD) một góc 300. Tính thể tích V của khối chóp đã cho.
-
Câu 31:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB = a, AD = 3a, BC = a. Biết SA = \(a\sqrt 3 \), tính thể tích khối chóp S.BCD theo a.
-
Câu 32:
Một khối lăng trụ tam giác có đáy là tam giác đều cạnh bằng 3, cạnh bên bằng tạo với mặt phẳng đáy một góc 300. Khi đó thể tích của khối lăng trụ là:
-
Câu 33:
Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a bằng:
-
Câu 34:
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc bằng 450. Thể tích của khối chóp S.ABC, tính theo a, là:
-
Câu 35:
Thể tích của khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a, A'B = 2a.
-
Câu 36:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc BAD = 450, tam giác SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của hình chóp S.ABCD là:
-
Câu 37:
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng (ABC). Thể tích khối chóp S.ABC bằng:
-
Câu 38:
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, biết A'A = A'B = A'C = a. Tính thể tích khối lăng trụ ABC.A'B'C'.
-
Câu 39:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 600. Tính thể tích khối chóp S.ABCD.
-
Câu 40:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, BCC'B', CDD'C' lần lượt là 2a2, 3a2, 6a2. Tính thể tích khối hộp chữ nhật ABCD.A'B'C'D'.
-
Câu 41:
Cho hình lập phương ABCD.A'B'C'D' có diện tích tam giác ACD' bằng \({a^2}\sqrt 3 \). Tính thể tích V của hình lập phương.
-
Câu 42:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và AB ⊥ (SBC) . Biết SB = \(2a\sqrt 3 \) và \(\widehat {SBC} = {30^0}\). Thể tích khối chóp S.ABC bằng:
-
Câu 43:
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H).
-
Câu 44:
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, cạnh bên bằng a√3a3. Diện tích toàn phần S của lăng trụ là:
-
Câu 45:
Nếu ba kích thước của một khối hộp chữ nhật tăng lên 4 lần thì thể tích của nó tăng lên bao nhiêu lần?
-
Câu 46:
Cho một khối chóp có chiều cao bằng h và diện tích đáy bằng B. Nếu giữ nguyên chiều cao h, còn diện tích đáy tăng lên 3 lần thì ta được một khối chóp mới có thể tích là:
-
Câu 47:
Cho khối chóp S.ABC có SA vuông góc với đáy, SA = a, tam giác ABC vuông tại A, AB = a, AC = 2a. Thể tích của khối chóp S.ABC bằng:
-
Câu 48:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a, SA =a. Tính thể tích khối chóp S.ABCD.
-
Câu 49:
Nếu tăng chiều dài hai cạnh đáy của khối hộp chữ nhật lên 10 lần thì thể tích tăng lên bao nhiêu lần?
-
Câu 50:
Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tính thể tích V của hình chóp S.ABCD biết AB = a, AD = 3a, SA = 2a.











