Trắc nghiệm Khái niệm về thể tích của khối đa diện Toán Lớp 12
-
Câu 1:
Tính thể tích V của khối lập phương ABCD.A’B’C’D’. Biết \(AC’ = a\sqrt 3 \)
-
Câu 2:
Cho hình lập phương ABCD.A’B’C’D’ có diện tích mặt chéo ACC’A’ bằng \(2\sqrt 2 {a^2}\). Thể tích của khối lập phương ABCD.A’B’C’D’ là.
-
Câu 3:
Khối lập phương có đường chéo bằng 2a thì có thể tích là.
-
Câu 4:
Cho hình lập phương có cạnh bằng 1. Diện tích của mặt cầu ngoại tiếp hình lập phương đó bằng
-
Câu 5:
Tính theo a thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC’ = a.
-
Câu 6:
Một hình lập phương có tổng diện tích các mặt bằng \(54{\rm{ c}}{{\rm{m}}^{\rm{2}}}\), thể tích của khối lập phương đó bằng
-
Câu 7:
Cho hình lập phương có tổng diện tích các mặt bằng \(12{{\rm{a}}^2}\). Thể tích khối lập phương đó bằng
-
Câu 8:
Gọi V là thể tích khối lập phương ABCD.A’B’C’D’, V’ là thể tích khối tứ diện A’.ABD. Hệ thức nào dưới đây là đúng?
-
Câu 9:
Một khối lập phương có thể tích bằng \(3\sqrt 3 {a^3}\) thì cạnh của khối lập phương đó bằng
-
Câu 10:
Tính thể tích V của khối lập phương \(ABCD.{A_1}{B_1}C{}_1{D_1}\), biết diện tích mặt chéo \(AC{C_1}{A_1}\) bằng \(4\sqrt 2 {a^2}\)
-
Câu 11:
Diện tích toàn phần của một hình hộp chữ nhật là \(S = 8{a^2}\). Đáy của nó là hình vuông cạnh a. Tính thể tích V của khối hộp theo a.
-
Câu 12:
Độ dài đường chéo của một hình lập phương bằng 3a. Tính thể tích V của khối lập phương.
-
Câu 13:
Cho hình lập phương ABCD.A’B’C’D’. Tính thể tích V của hình lập phương biết rằng khoảng cách từ trung điểm I của AB đến mặt phẳng \(\left( {A’B’CD} \right)\) bằng \(\frac{a}{{\sqrt 2 }}\)
-
Câu 14:
Thể tích của khối lập phương ABCD.A’B’C’D’ với AD’ = 3a.
-
Câu 15:
Cho khối chóp có đáy là hình vuông cạnh \(a\sqrt 2 \) và chiều cao 3a. Thể tích V của khối chóp đã cho bằng:
-
Câu 16:
Tổng diện tích các mặt của hình lập phương bằng 54.Thể tích của khối lập phương là:
-
Câu 17:
Cho hình lập phương ABCD.A’B’C’D’ với O’ là tâm hình vuông A’B’C’D’. Biết rằng tứ diện O’.BCD có thể tích bằng \(6{a^3}\). Tính thể tích V của khối lập phương ABCD.A’B’C’D’.
-
Câu 18:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh 2a và A’B = 3a. Tính thể tích khối hộp chữ nhật ABCD.A’B’C’D’ theo a.
-
Câu 19:
Tính thể tích khối lập phương ABCD.A’B’C’D’ biết \(BD’ = \sqrt 3 a.\)
-
Câu 20:
Diện tích toàn phần của khối lập phương bằng \(96\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\). Khi đó thể tích khối lập phương là
-
Câu 21:
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Biết AB = a, AD = 2a, AA’ = 3a. Tính thể tích khối hộp ABCD.A’B’C’D’.
-
Câu 22:
Thể tích của khối lập phương cạnh 2a bằng
-
Câu 23:
Cho hình lập phương có thể tích bằng 8. Diện tích toàn phần của hình lập phương là
-
Câu 24:
Một hộp đựng thực phẩm có dạng hình lập phương và có diện tích toàn phần bằng \(150{\rm{ c}}{{\rm{m}}^2}\). Thể tích của khối hộp là:
-
Câu 25:
Cho \(\left( H \right)\) là khối lập phương có độ dài cạnh bằng \(3\left( {cm} \right)\). Thể tích của \(\left( H \right)\) bằng
-
Câu 26:
Gọi \(l, h, R\) lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón. Đẳng thức nào sau đây đúng?
-
Câu 27:
Cho hình nón có bán kính đường tròn đáy bằng R, chiều cao bằng h, độ dài đường sinh bằng \(l\). Khẳng định nào sau đây là đúng?
-
Câu 28:
Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy là tam giác đều cạnh \(2 a \sqrt{2}\) và \(A^{\prime} A=a \sqrt{3}\). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Thể tích của khối lăng trụ đã cho bằng
-
Câu 29:
Cho lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết \(A^{\prime} O=a\) . Thể tích của khối lăng trụ đã cho bằng
-
Câu 30:
Cho hình hộp chữ nhật có đường chéo \(d=\sqrt{21}\). Độ dài ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân có công bội q = 2. Thể tích của khối hộp chữ nhật đã cho bằng
-
Câu 31:
Cho khối hộp đứng có đáy là một hình thoi có độ dài đường chéo nhỏ bằng 10 và góc nhọn bằng 60o. Diện tích mỗi mặt bên của khối hộp bằng 10. Thể tích của khối hộp đã cho bằng
-
Câu 32:
Cho hình hộp chữ nhật có diện tích ba mặt cùng xuất phát từ cùng một đỉnh là \(10 \mathrm{cm}^{2}, 20 \mathrm{cm}^{2}, 32 \mathrm{cm}^{2}\) Thể tích của khối hộp chữ nhật đã cho bằng
-
Câu 33:
Cho khối hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { có } A A^{\prime}=a \sqrt{3}\) Biết rằng mặt phẳng (A'BC) hợp với mặt đáy (ABCD) một góc 600 đường thẳng A'C hợp với mặt đáy (ABCD) một góc 300 .Thể tích của khối hộp chữ nhật đã cho bằng
-
Câu 34:
Cho lăng trụ đứng ABC .A'B'C' có AA'= 3. Tam giác A'BC có diện tích bằng 6 và tạo với mặt đáy (ABC) góc 600 .Thể tích của khối lăng trụ đã cho bằng
-
Câu 35:
Cho khối lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác cân với \(A B=A C=a, \widehat{B A C}=120^{\circ}\) Mặt phẳng \(\left(A B^{\prime} C^{\prime}\right)\) tạo với đáy một góc 600 Thể tích của khối lăng trụ đã cho bằng
-
Câu 36:
Cho hình hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có \(A B=A A^{\prime}=a\), đường chéo A'C tạo với mặt đáy (ABCD) một góc \(\alpha\) thỏa \(\cot \alpha=\sqrt{5}\) Thể tích khối hộp đã cho bằng
-
Câu 37:
Cho lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại B và B A=B C=1. Cạnh A'B tạo với mặt đáy (ABC) góc \(60^{\circ}\) Thể tích của khối lăng trụ đã cho bằng
-
Câu 38:
Cho hình hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { có } A B=a, A D=2 a, A C^{\prime}=\sqrt{6} a\) . Thể tích khối hộp bằng
-
Câu 39:
Cho khối lập phương ABCD. A' B' C' D có độ dài đường chéo \(A^{\prime} C=a \sqrt{3}\). Thể tích của khối lập phương đã cho bằng
-
Câu 40:
Cho hình hộp chữ nhật \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { có } B A=a, B C=a \sqrt{2}, B A^{\prime}=a \sqrt{5}\) .Thể tích của khối hộp đã cho bằng
-
Câu 41:
Cho khối lăng trụ tam giác đều có cạnh đáy bằng a và tổng diện tích các mặt bên bằng 3a2 .Thể tích của khối lăng trụ đã cho bằng
-
Câu 42:
Cho lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác với \(AB=a, A C=2 a, \widehat{B A C}=120^{\circ} \text { và } A A^{\prime}=2 a \sqrt{5}\). Thể tích của khối lăng trụ đã cho bằng
-
Câu 43:
Cho khối lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có BB'=a , đáy ABC là tam giác vuông cân tại B và \(A C=a \sqrt{2}\). Thể tích của khối lăng trụ đã cho bằng
-
Câu 44:
Cho hình lăng trụ đứng ABCD. A' B' C' D' có \(A A^{\prime}=3 a, A C=4 a, B D=5 a\) , ABCD là hình thoi. Thể tích của khối lăng trụ đã cho bằng
-
Câu 45:
Cho khối hộp chữ nhật ABCDA'B'C'D' có \(A A^{\prime}=a, A B=3 a, A C=5 a\) . Thể tích của khối hộp đã cho bằng
-
Câu 46:
Cho khối lăng trụ đứng ABC A' B' C' có đáy là tam giác đều cạnh a và \(A A^{\prime}=\sqrt{3} a\)3 . Thể tích của khối lăng trụ đã cho bằng
-
Câu 47:
Khối lăng trụ tam giác đều có tất cả các cạnh bằng a có thể tích bằng
-
Câu 48:
Cho khối chóp tứ giác đều S.ABCD . có đáy là hình vuông tâm O, cạnh bằng a. Cạnh bên bằng \(a \sqrt{3}\). Gọi M là trung điểm của CD, H là điểm đối xứng của O qua SM (tham khảo hình vẽ bên). Thể tích khối đa diện ABCDSH bằng
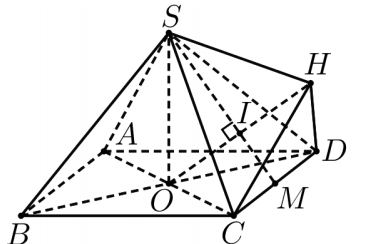
-
Câu 49:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng \(\frac{a \sqrt{2}}{2}\) Thể tích của khối chóp đã cho bằng
-
Câu 50:
Cho hình chóp S.ABCD có đáy là hình vuông. Cạnh bên SA vuông góc với mặt phẳng đáy và SA=a . Diện tích tam giác SBC bằng \(\frac{a^{2} \sqrt{2}}{2}\) Thể tích khối chóp đã cho bằng











