Trắc nghiệm Khoảng cách Toán Lớp 11

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên của hình chóp bằng nhau và bằng 2a. Tính khoảng cách d từ A đến mặt phẳng ( SCD )

Câu 2:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(AB = a,AC = a\sqrt 3\) . Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách d từ B đến mặt phẳng (SAC)

Câu 3:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SBvuông góc với mặt phẳng đáy. Cho biết SB = 3a , AB = 4a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)

Câu 4:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên \(SA = a\sqrt 3\) và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC)

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60⁰. Gọi M là trung điểm của cạnh AB. Tính khoảng cách d  từ B đến mặt phẳng (SMC)

Câu 6:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC) 

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \( SA = \frac{{a\sqrt {15} }}{2}\) và vuông góc với mặt đáy (ABCD). Tính khoảng cách d  từ O đến mặt phẳng (SBC).

Câu 8:

Cho hình chóp S.ABCD có đáy (ABCD ) là hình chữ nhật. Tam giác (SAB ) đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD) . Biết \(SD = 2a\sqrt3\) và góc tạo bởi đường thẳng (SC ) và mặt phẳng (ABCD) bằng 30⁰. Tính khoảng cách từ điểm B đến mặt phẳng (SAC)

Câu 9:

Cho hình chóp S.ABCD có đáy (ABCD ) là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 60⁰ . Tính khoảng cách d từ điểm D đến mặt phẳng (SBC)

Câu 10:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Biết \(SA = \sqrt3 a \) và SA vuông góc (ABCD). Gọi H là hình chiếu vuông góc của A trên (SBC) Tính khoảng cách d từ H đến mặt phẳng SCD

Câu 11:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a, H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD Tính khoảng cách từ điểm A đến mặt phẳng (SCD).

Câu 12:

Cho hình chóp (S.ABCD ) có đáy ABCD là hình vuông,  \(\frac{{SB}}{{\sqrt 2 }} = \frac{{SC}}{{\sqrt 3 }} = a\). Cạnh SA vuông góc (ABCD), khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \( AB = a\sqrt 2 \). Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ D đến mặt phẳng (SBC)

Câu 14:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên \( SA = a\sqrt 2 \) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)

Câu 15:

Cho hình chóp S.ABC có đáy ABC là tam giác cạnh \(BC = a, AC = 2a\sqrt2 , \widehat{ACB} = 45^0\). Cạnh bên SB vuông góc với mặt phẳng (ABC). Tính khoảng cách từ điểm A đến mặt phẳng (SBC).

Câu 16:

Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC' bằng nhau ?

Câu 17:

Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB' bằng

Câu 18:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng

Câu 19:

Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng

Câu 20:

Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết \( SA = 3a, AB = a\sqrt 3 , BC = a\sqrt 6\) . Khoảng cách từ B đến SC bằng

Câu 21:

Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng alpha . Khoảng cách từ tâm của đáy đến một cạnh bên bằng

Câu 22:

Cho hình chóp S.ABCD có SA vuông góc (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.

Câu 23:

Cho hình chóp S.ABCDcó SA vuông góc (ABCD), đáy ABCD là hình thoi cạnh bằng a và \(\hat B = 60^0\) . Biết SA = 2a. Tính khoảng cách từ A đến SC.

Câu 24:

Cho hình chóp A.BCDcó cạnh AC vuông góc BCD và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) , khoảng cách từ A đến đường thẳng BD bằng:

Câu 25:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách từ M đến SA nhận giá trị nào trong các giá trị sau?

Câu 26:

Hình chóp đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là trung điểm của BC, khoảng cách từ S đến AH bằng:

Câu 27:

Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

Câu 28:

Cho tứ diện SABC trong đóSA, SB, SC vuông góc với nhau từng đôi một vàSA = 3a, SB = a,SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

Câu 29:

Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD  là tam giác đều cạnh bằng a. Biết \( AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

Câu 30:

Cho hình chóp S.ABCD trong đó SA, AB, BC đôi một vuông góc và SA = AB = BC = 1. Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau ?

Câu 31:

Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Tính khoảng cách giữa đường thẳng MN và (ABC).

Câu 32:

Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60^o. Tam giác ABC cân ở C, tam giác ABD cân ở D. Đường cao DK của tam giác ABD bằng 12cm. Khoảng cách từ D đến (ABC) bằng giá trị nào dưới đây?

Câu 33:

Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến (BCD) bằng bao nhiêu?

Câu 34:

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng A. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC' bằng nhau?

Câu 35:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến (SAB) nhận giá trị nào trong các giá trị sau?

Câu 36:

Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng bao nhiêu?

Câu 37:

Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a². Khoảng cách từ S đến BC bằng bao nhiêu?

Câu 38:

Trong các mệnh đề sau, mệnh đề nào đúng?

Câu 39:

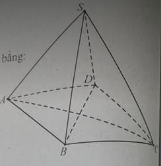
Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.

Khoảng cách từ D đến mặt phẳng (SAC) bằng:

Câu 40:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Giả sử góc BAD bằng 60^o. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng: