Cho hàm số f(x)có bảng xét dấu đạo hàm như sau
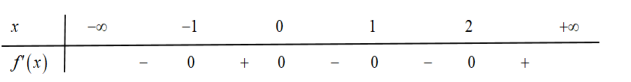
Hàm số \(y=6 f(x-1)-2 x^{3}+3 x^{2}\) đồng biến trên khoảng nào dưới đây?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(y^{\prime}=6 \cdot f^{\prime}(x-1)-6 x^{2}+6 x \cdot y^{\prime}=0 \Leftrightarrow f^{\prime}(x-1)=x^{2}-x\)
Đặt \(t=x-1 \Rightarrow x=t+1\)
Khi đó ta có phương trình \(f^{\prime}(t)=(t+1)^{2}-(t+1) \Leftrightarrow f^{\prime}(t)=t^{2}+t(*)\)
Nhận thấy phương trình (*) có nghiệm \(t=0 ; t=-1\)
Trên khoảng \((-1 ; 0) \text { thì } f^{\prime}(t)>0 \text { và } t^{2}+t<0 \text { nên } f^{\prime}(t)-\left(t^{2}+t\right)>0\)
Nên hàm số y(t) đồng biến trên khoảng (-1;0) .
Suy ra hàm số (x) đồng biến trên khoảng (0;1)
ADMICRO
YOMEDIA
ZUNIA9
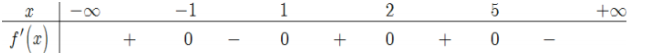
.png)