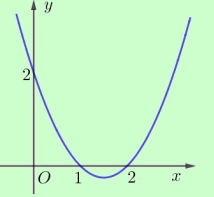
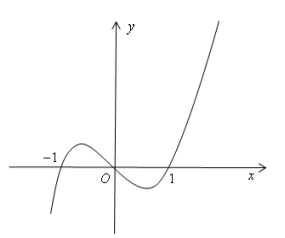
Cho hàm số f (x) có đồ thị của f'(x) như hình vẽ bên. Có bao nhiêu số nguyên \(m \in[-5 ; 5]\) để hàm số \(f(x+m)\) nghịch biến trên khoảng (1 ; 2) ?
.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(g(x)=f(x+m) . \text { Та } \operatorname{có} g^{\prime}(x)=f^{\prime}(x+m)\)
Yêu cầu bài toán \( \Leftrightarrow f^{\prime}(x+m) \leq 0, \forall x \in(1 ; 2)\)
\(\begin{array}{l} \Leftrightarrow f^{\prime}(t) \leq 0, \forall t \in(1+m ; 2+m) \text { vói } t=x+m \\ \Leftrightarrow\left[\begin{array}{l} 2+m \leq-1 \\ 1 \leq 1+m<2+m \leq 3 \end{array} \Leftrightarrow\left[\begin{array}{l} m \leq-3 \\ m \geq 0 \\ m \leq 1 \end{array} \Leftrightarrow\left[\begin{array}{l} m \leq-3 \\ 0 \leq m \leq 1 \end{array}\right.\right.\right. \end{array}\)
Vì \(m \in[-5 ; 5] \text { nên } m \in\{-5 ;-4 ;-3 ; 0 ; 1\}\)
Vậy có 5 giá trị m thỏa điều kiện.
.png)