Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không có nắp đủ chứa được10 lít nước. Hỏi bán kính đáy (đơn vị cm, làm tròn đến hàng phần chục) của chiếc xô bằng bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi x ( x > 0 ) là bán kính của chiếc xô. Khi đó \(V=\pi x^{2} h \Rightarrow h=\frac{V}{\pi x^{2}}\) .
Để tiết kiệm nguyên vật liệu thì diện tích toàn phần của chiếc xô phải bé nhất. Ta có: \(10 l=10 d m^{3}=10000 c m^{3}\)
Diện tích toàn phần của chiếc xô là: \(S(x)=\pi x^{2}+2 \pi x h=\pi x^{2}+2 \pi x \frac{V}{\pi x^{2}}=\pi x^{2}+2 \frac{10000}{x}=\pi x^{2}+\frac{20000}{x}\)
\(\begin{array}{l} S^{\prime}(x)=2 \pi x-\frac{20000}{x^{2}}=\frac{2 \pi x^{3}-20000}{x^{2}} \\ S^{\prime}(x)=0 \Leftrightarrow 2 \pi x^{3}-20000=0 \Leftrightarrow x^{3}=\frac{10000}{\pi} \Leftrightarrow x=10 \sqrt[3]{\frac{10}{\pi}} \end{array}\)
Bảng biến thiên
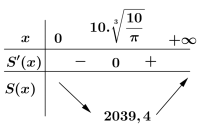
Ta thấy diện tích toàn phần chiếc xô nhỏ nhất khi bán kính đáy xô là \(x=10 \sqrt[3]{\frac{10}{\pi}} \approx 14,7(\mathrm{cm})\)
Câu hỏi liên quan
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x}{x-m}\) đồng biến trên khoảng \((1 ;+\infty)\)
-
Giá trị của tham số m để \(f(x)=2 m x^{3}-6 x^{2}+(2 m-4) x+3+m\) nghịch biến trên R là?
-
Hàm số \(y = - {x^3} - 2{x^2} + 3x\) nghịch biến trên khoảng nào sau đây?
-
Tìm khoảng đồng biến của hàm số \(y = 2{x^3} - 9{x^2} + 12x + 3\)
-
Cho hàm số \(y=|x+1|(x-2)\) Khẳng định nào sau đây là khẳng định sai?
-
Cho hàm số \(y=\frac{m x+9}{x+m}\) ( m là tham số thực). Tìm các giá trị của m để hàm số đã cho nghịch biến trên khoảng \((-\infty ; 1) ?\)
-
Cho hàm số \(y=x^{3}+2(m+1) x^{2}-3 m x+5-m\) với m là tham số. tìm diều kiện của m đẻ hàm số đồng biến trên tập xác định?
-
Hàm số \(y = {x^3} + 8{x^2} + 3x - 2\) đồng biến trên khoảng nào sau đây?
-
Tìm các giá trị của tham số m để hàm số \(y=\frac{x+6}{x-m}\)( m là tham số thực) nghịch biến trên khoảng \((4 ;+\infty) ?\)
-
Hàm số \(y = - {x^3} - 2{x^2} + 3x\) đồng biến trên khoảng nào sau đây?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y\; = \;\frac{{x - m + 2}}{{x + 1}}\) giảm trên các khoảng mà nó xác định ?
-
Tập hợp các giá trị thực của tham số m để hàm số \(y = x + 1 + \frac{m}{{x – 2}}\) đồng biến trên mỗi khoảng xác định của nó là
-
Tìm tham số m để hàm số \(y=\frac{\sin x+4}{\sin x+m}\) nghịch biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\)?
-
Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
-
Cho hàm số \(y = \frac{{\ln x – 4}}{{\ln x – 2m}}\) với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của S.
-
Cho hàm hàm số y =f(x) có bảng biến thiên như hình vẽ dưới
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(\left|f\left(x^{2}+1\right)\right|=m\) có 6 nghiệm phân biệt
-
Cho hàm số \(y=-x^{3}-m x^{2}+(4 m+9) x+5\) (với m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên R ?
-
Hỏi hàm số \(y\; = \;\frac{3}{5}{x^5}\; - \;3{x^4}\; + \;4{x^3}\; - \;2\) đồng biến trên khoảng nào?
-
Cho hàm số \(y\; = \;x\; + \;{\cos ^2}\left( x \right)\). Khẳng định nào sau đây là khẳng định đúng?
-
Hàm số y = x3 – 3x đồng biến trên khoảng nào?
