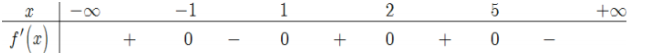Tìm tất cả các giá trị của m để hàm số \(y=2^{x^{3}-x^{2}+m x}\) đồng biến trên \([1,2]\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y^{\prime}=\left(3 x^{2}-2 x+m\right) 2^{x^{3}-x^{2}+m x} \ln 2\)
Hàm số đã cho đồng biến trên \([1,2] \Leftrightarrow y^{\prime} \geq 0, \forall x \in[1,2] \Leftrightarrow 3 x^{2}-2 x+m \geq 0, \forall x \in[1,2]\left(^{*}\right)\)
Vì \(f(x)=3 x^{2}-2 x+m \text { có } a=3>0,-\frac{b}{2 a}=\frac{1}{3}<2\) nên
\(\begin{array}{l} (*) \Leftrightarrow \left[ \begin{array}{l} {\Delta ^\prime } \le 0\\ \left\{ \begin{array}{l} {\Delta ^\prime } > 0\\ \begin{array}{*{20}{l}} {\frac{{{x_1} + {x_2}}}{2} < 1}\\ {\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) \ge 0} \end{array} \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 1 - 3m \le 0\\ \left\{ {\begin{array}{*{20}{l}} {1 - 3m > 0}\\ {\frac{1}{3} < 1}\\ {\frac{m}{3} - \frac{2}{3} + 1 \ge 0} \end{array}} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} m \ge \frac{1}{3}\\ \left\{ {\begin{array}{*{20}{l}} {m < \frac{1}{3}}\\ {m \ge - 1} \end{array}} \right. \end{array} \right. \Rightarrow m \ge - 1\\ \end{array}\)
.png)