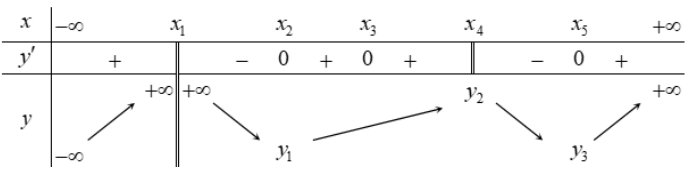Cho hàm số \(y = f\left( x \right)\) liên tục và xác định trênvà có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để hàm số \(y = \left| {{{\left( {f\left( x \right)} \right)}^2} + 2mf\left( x \right) + 2m + 35} \right|\) có đúng 3 điểm cực trị
.jpg.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số: \(g\left( x \right) = {\left( {f\left( x \right)} \right)^2} + 2mf\left( x \right) + 2m + 35 \Rightarrow g’\left( x \right) = f’\left( x \right).\left( {2f\left( x \right) + 2m} \right)\)
Cho: \(g’\left( x \right) = f’\left( x \right).\left( {2f\left( x \right) + 2m} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f'(x) = 0 \Leftrightarrow x = – 4\;;\;x = 1}\\{f(x) = – m{\rm{ }}}\end{array}} \right.\)
* \(f'(x) = 0 \Leftrightarrow x = – 4\;;\;x = 1 \Rightarrow\) có thêm hai điểm cực trị.
* \(f(x) = – m{\rm{ }} \Rightarrow \) có ít nhất một nghiệm đơn
Đã biết hàm số \(y = \left| {g\left( x \right)} \right|\) có số cực trị bằng tổng số điểm cực trị hàm số \(y = g\left( x \right)\) và số nghiệm đơn của phương trình \(g\left( x \right) = 0\).
Để hàm số \(y = \left| {g\left( x \right)} \right|\) có đúng 3 điểm cực trị thì ta phải có:
\(\left\{ {\begin{array}{*{20}{c}}{f\left( x \right) = – m{\rm{ co dung mot nghiem don}}{\rm{. }}}\\{g\left( x \right) = {{\left( {f\left( x \right)} \right)}^2} + 2mf\left( x \right) + 2m + 35 = 0{\rm{ khong}}\,{\rm{co nghiem phan biet }}}\end{array}}\right.\)
\(\left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{ – m \ge 3}\\{ – m \le – 5}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \le – 3}\\{m \ge 5}\end{array}} \right.} \right.}\\{\Delta ‘ = {m^2} – 2m – 35 \le 0 \Leftrightarrow – 5 \le m \le 7}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ – 5 \le m \le – 3}\\{5 \le m \le 7}\end{array} \Rightarrow m = \left\{ { – 5\;;\; – 4\;;\; – 3\;;\;5\;;\;6\;;\;7} \right\}} \right.} \right.\)
Suy ra có 6 giá trị m nguyên thỏa mãn.
Câu hỏi liên quan
-
Số cực trị của hàm số \(f\left( x \right) = 4{{\rm{x}}^4} + {{\rm{x}}^2} + 4\) là
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên R, có đạo hàm trên R và có bảng biến thiên như hình vẽ bên.
.png)
Khẳng định nào sau đây là sai?
-
Giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = {x^3} – 3{x^2} + 7\) là
-
Tìm tất cả các giá trị của tham số m để hàm số \(y = {x^3} - m{x^2} + \left( {2m - 3} \right)x - 3\) đạt cực đại tại x = 1
-
Hàm số nào trong các hàm số sau đây không có cực trị?
-
Điểm cực tiểu của đồ thị hàm số \(y = - {x^4} + 2{x^2} + 2\) là:
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
-
Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=|f(x)|
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = - 4{{\rm{x}}^4} - 2{{\rm{x}}^2} + 4\) là
-
Cho hàm số y=f(x) có đồ thị như hình bên dưới. Đồ thị hàm số \(g(x)=f(|x|-2)\) có bao nhiêu điểm cực trị ?
-
Hàm số \(y = {x^3} – 3x\) đạt cực tiểu tại x bằng?
-
Tìm số điểm cực trị của hàm số y = x4 – 2x2 + 2
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}+\left(m^{2}-m+2\right) x^{2}+\left(3 m^{2}+1\right) x\) đạt cực tiểu tại x=-2?
-
Số điểm cực tiểu của hàm số \(f(x)=\frac{1}{4} x^{4}+\frac{1}{2} x^{2}+3\) là
-
Tìm giá trị cực đại yCĐ của hàm số y = −x4+2x2−5
-
Cho hàm số \(y=(m-1) x^{4}-3 m x^{2}+5\) . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
-
Điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{4}{x^4} + 2{x^2} - 2\) là:
-
Cho hàm số \(y = {x^4} + 4{x^2} + 2\). Mệnh đề nào dưới đây là mệnh đề đúng?
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = x⁸ + (m -1)x⁵ - (m² -1)x⁴ +1 \) đạt cực tiểu taị x=0
-
Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là
