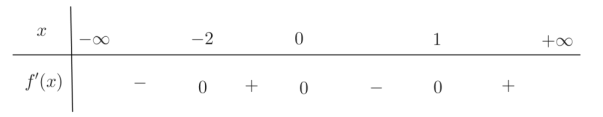Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x x^{2}(x-1)\left(x^{2}+m x+5\right)\). Có bao nhiêu số nguyên âm m để hàm số \(y=f\left(x^{2}\right)\)đồng biến trên khoảng \((1 ;+\infty)\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y^{\prime}=2 x f^{\prime}\left(x^{2}\right)=2 x\left(x^{2}\right)^{2}\left(x^{2}-1\right)\left(x^{4}+m x^{2}+5\right)=2 x^{5}\left(x^{2}-1\right)\left(x^{4}+m x^{2}+5\right)\)
Yêu cầu bài toán \(\Leftrightarrow y^{\prime} \geq 0, \quad \forall x>1 \Leftrightarrow 2 x^{5}\left(x^{2}-1\right)\left(x^{4}+m x^{2}+5\right)\)
\(\forall x>1 \Leftrightarrow x^{4}+m \mathrm{x}^{2}+5 \geq 0, \forall x>1 \Leftrightarrow m \geq-\frac{x^{4}+5}{x^{2}}, \forall x>1\)
Đặt \(g(x)=-\frac{x^{4}+5}{x^{2}}=-\left(x^{2}+\frac{5}{x^{2}}\right)\)
Ta có:
\(x^{2}+\frac{5}{x^{2}} \geq 2 \sqrt{5} \Rightarrow g(x) \leq-2 \sqrt{5}, \forall x>1 \Rightarrow \operatorname{Max}_{(1 ;+\infty)} g(x)=-2 \sqrt{5} \text { khi } x=\sqrt[4]{5}\)
\(m \geq-\frac{x^{4}+5}{x^{2}}=g(x), \forall x>1 \Rightarrow m \geq \operatorname{Max}_{(1 ;+\infty)} g(x)=-2 \sqrt{5} \simeq-4,4\)
Vậy có 4 giá trị nguyên âm của m thỏa mãn yêu cầu bài toán.
Câu hỏi liên quan
-
Có bao nhiêu giá trị nguyên dương của tham số m sao cho để hàm số \(f(x)=-\frac{1}{3} x^{3}-(m-1) x^{2}+(m-7) x-2\) nghịch biến trên \(\mathbb{R}\)?
-
Hàm số \(y=\frac{1}{3} x^{3}+(m+1) x^{2}-(m+1) x+1\) đồng biến trên tập xác định của nó khi?
-
Hàm số nào sau đây đồng biến trên tập số thực R?
-
Cho hàm số \(y = f(x) = 2{x^3} + 6{x^2} + 6x - 2017\). Mệnh đề nào dưới đây sai
-
Cho hàm số \(y=(m+2) \frac{x^{3}}{3}-(m+2) x^{2}+(m-8) x+m^{2}-1\) . Có bao nhiêu giá trị nguyên của \(m\in(-10;0)\) để hàm số nghịch biến trên \(\mathbb{R}\)?
-
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số \(y = \ln \left( {{x^2} + 1} \right) - mx + 1\) đồng biến trên khoảng ( -∞; +∞).
-
Bất phương trình \(\sqrt {{x^2} - 2x + 3} - \sqrt {{x^2} - 6x + 11} > \sqrt {3 - x} - \sqrt {x - 1} \) có tập nghiệm (a; b]. Hỏi hiệu b-a có giá trị là bao nhiêu?
-
Hàm số \(y = {x^3} - 5{x^2} + 5\) nghịch biến trên các khoảng:
-
Hàm số y = - x3 + 3x – 5 đồng biến trên khoảng nào sau đây?
-
Cho hàm số \(y=-x^{3}-m x^{2}+(4 m+9) x+5\) (với m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên R ?
-
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R. Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi hàm số y=f(3x–9) đồng biến trong khoảng nào sau đây?
.png)
-
Hỏi hàm số \(y\; = \;\frac{3}{5}{x^5}\; - \;3{x^4}\; + \;4{x^3}\; - \;2\) đồng biến trên khoảng nào?
-
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = \frac{1}{4}{x^4} + mx – \frac{3}{{2x}}\) đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\)
-
Hàm số nào sau đây đồng biến trên R.
-
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0.
-
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{{x^2}}}{2} - 6x + \frac{3}{4}\). Chọn khẳng định đúng.
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
-
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) là đúng?
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{\cot x-1}{m \cot x-1}\) đồng biến trên khoảng \(\left(\frac{\pi}{4} ; \frac{\pi}{2}\right)\)
-
Tìm giá trị nhỏ nhất của tham số m sao cho hàm số \(y=\frac{x^{3}}{3}+m x^{2}-m x-m\) luôn đồng biến trên \(\mathbb{R}\) ?
