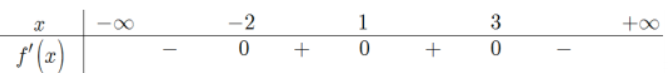Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
Hàm số \(g(x)=\left(\frac{1}{2}\right)^{f(1-2 x)}\) nghịch biến trên khoảng nào dưới đây
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: \(\mathbb{R}\)
\(g^{\prime}(x)=(1-2 x)^{\prime} \cdot f^{\prime}(1-2 x) \cdot\left(\frac{1}{2}\right)^{f(1-2 x)} \cdot \ln \left(\frac{1}{2}\right)=g^{\prime}(x)=2 \ln 2 \cdot f^{\prime}(1-2 x) \cdot\left(\frac{1}{2}\right)^{f(1-2 x)}\)
Hàm số đông biến khi \(g^{\prime}(x)<0 \Leftrightarrow f^{\prime}(1-2 x)<0\)
Từ đồ thị của hàm số y=f'(x) ta thấy
\(f^{\prime}(1-2 x)<0 \Leftrightarrow\left[\begin{array}{l} 1-2 x<-1 \\ 1<1-2 x<2 \end{array} \Leftrightarrow\left[\begin{array}{l} x>1 \\ -\frac{1}{2}<x<0 \end{array}\right.\right.\)
Hay \(g^{\prime}(x)<0 \Leftrightarrow\left[\begin{array}{l} x>1 \\ -\frac{1}{2}<x<0 \end{array}\right.\)
Như vậy trên mỗi khoảng \(\left(-\frac{1}{2} ; 0\right),(1 ;+\infty)\) hàm số y =g(x) nghịch biến.
So sánh các phương án ta thấy phương án D thỏa .yêu cầu đề bài.