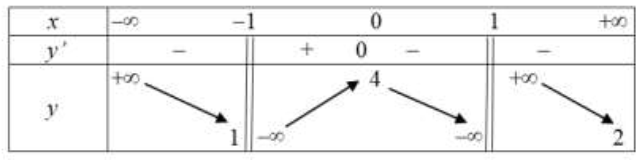
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới:

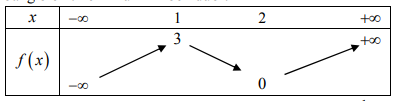
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2 f(x)-1}\) là

Câu hỏi liên quan

• Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+4}-2}{x^{2}+x}\) là: 

• Tổng số các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{x^{3}-2 x^{2}}\) là?

• Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sau đây?

ZUNIA12

• Đồ thị hàm số \(y=\frac{x+2}{3 x+9}\) có đường tiệm cận đứng là x=a và đường tiệm cận ngang là y=b. Giá trị của số nguyên m nhỏ nhất thỏa mãn \(m \geq a+b\) là 

• Cho hàm số y = f( x ) có bảng biến thiên như sau:

  

  Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số\( y = \frac{1}{{f\left( x \right) - 1}}\)

• Đồ thị hàm số \(y=\frac{2 x-3}{x-1}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
   

• Đồ thị hàm số \(y=\frac{1-3 x^{2}}{x^{2}-6 x+9}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

• Đồ thị hàm số \(y = \dfrac{{ - 4}}{{x + 1}}\) có đường tiệm cận đứng là:

• Cho hàm số \(y = \frac{{x - 2}}{{3 - 2x}}\) có đồ thị (C). Tìm khẳng định đúng.

• Cho hàm số \(y=\frac{2 x-3}{x-2}(C)\). Gọi M là điểm bất kỳ trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là 

• Cho hàm số \(y=\frac{x-1}{x+m}(m \neq-1)\) có đồ thị là (C) . Tìm để đồ thị (C) nhận điểm I(2;1) làm tâm đối xứng.

• Đồ thị hàm số \(y=\frac{3 x-1}{3 x+2}\) có đường tiệm cận ngang là

• Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+4}-2}{x^{2}+x}\) là?

• Cho hàm số \( f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \( g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\) có bao nhiêu tiệm cận đứng?

  

• Có bao nhiêu giá trị m để đồ thị hàm số \(y=\frac{m x^{2}-1}{x^{2}-3 x+2}\) có đúng hai đường tiệm cận? 

• Đồ thị hàm số \(y=\frac{x^{2}+3}{x^{2}-2|x|-3}\) có tổng số tiệm cận đứng và tiệm cận ngang là?

• Số tiệm cận của đồ thị hàm số \(y=\left\{\begin{array}{l} \frac{\sqrt{x^{2}+1}}{x} \text { nếu } x \geq 1 \\ \frac{2 x}{x-1} \text { nếu } x<1 \end{array}\right.\)

• Tìm tất cả các tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x-1-\sqrt{x^{2}+x+3}}{x^{2}-5 x+6}\)

• Đồ thị hàm số \(y=\frac{2 x-1}{x+2}\) có bao nhiêu đường tiệm cận

• Cho hàm số y =f(x) có \(\lim \limits_{x \rightarrow 1^{+}} f(x)=-\infty \text { và } \lim \limits_{x \rightarrow-1^{-}} f(x)=+\infty\) . Khẳng định nào sau đây là khẳng định đúng?