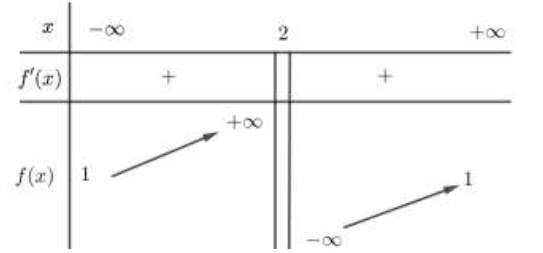
Cho hàm số y = f(x) xác định trên R\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

Câu hỏi liên quan

• Xác định m để đồ thị hàm số \(y=\frac{x^{2}-(2 m+3) x+2(m-1)}{x-2}\) không có tiệm cận đứng

• Số đường tiệm cận của đồ thị hàm số \(y=\frac{2}{x-9}\) là

• Cho hàm số \(y=f(x)\) có bảng biến thiên như sau: 

  

  Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình

ZUNIA12

• Đồ thị hàm số \(y=\frac{\sqrt{4-x^{2}}}{x^{2}-3 x-4}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang ? 

• Cho hàm số \(y = \dfrac{{3x - 1}}{{x + 4}}\). Gọi \(I\) là giao điểm của hai đường tiệm cận. Tính \(OI\).

• Đồ thị hàm số \(y=\frac{x-2}{x^{2}-4}\) có mấy tiệm cận?

• Đồ thị hàm số \(y=\frac{2 x-1}{x+2}\) có bao nhiêu đường tiệm cận

• Cho hàm số y=f(x) có \(\lim\limits _{x \rightarrow+\infty} f(x)=3 \text { và } \lim\limits _{x \rightarrow-\infty} f(x)=-3\) . Khẳng định nào sau đây là khẳng định đúng ?

• Số đường tiệm cận của đồ thị hàm số \(y=\frac{2-x}{1+|x|} \mid\) là?

• Đường tiệm cận ngang của đồ thị hàm số \(y=\frac{1}{x-2} \text { là }\)

• Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y=\frac{m x+1}{x+1}\) có hai đường tiệm cận là:
   

• Tìm tham số m để đồ thị hàm số \(y=\frac{(m+1) x-5 m}{2 x-m}\) có tiệm cận ngang là đường thẳng y=1 .

• Cho hàm số \( f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \( g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\) có bao nhiêu tiệm cận đứng?

  

• Số tiệm cận của đồ thị hàm số \(y=\left\{\begin{array}{l} \frac{\sqrt{x^{2}+1}}{x} \text { nếu } x \geq 1 \\ \frac{2 x}{x-1} \text { nếu } x<1 \end{array}\right.\)

• Đường tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x-2} 1 \) là:

• Tìm phương trình đường tiệm cận ngang của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiaadIhacqGHRaWkcaaIYaaabaGaamiEaiab % gUcaRiaaigdaaaaaaa!3DFA! y = \frac{{3x + 2}}{{x + 1}}\).

• Cho hàm số y=f(x) có báng biến thiên như sau:
  

  Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

• Cho hàm số y=f(x) có bảng biến thiên như sau

  
  Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:

• Tiệm cận đứng và ngang của đồ thị hàm số \( y = - \frac{3}{{x - 2}}\)

• Số đường tiệm cận của đồ thị hàm số \(y = \frac{{1 - x}}{{1 + x}}\) là