Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 5a , cạnh bên \(S A=10 a\) và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tính tan của góc tạo bởi hai mặt phẳng \((A M C) \text { và }(S B C)\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChuẩn hóa với a =1.
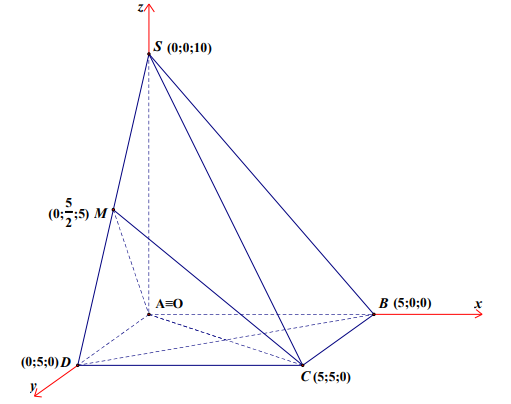
Xét hệ trục tọa độ Oxyz như hình vẽ sau:
Chọn hệ trục tọa độ như hình vẽ.
\(\begin{aligned} &A(0 ; 0 ; 0) ; D(0 ; 5 ; 0) ; B(5 ; 0 ; 0) ; C(5 ; 5 ; 0) ; S(0 ; 0 ; 10) ; M\left(0 ; \frac{5}{2} ; 5\right)\\ &\overrightarrow{B C}=(0 ; 5 ; 0), \overrightarrow{B S}=(-5 ; 0 ; 10)\\ &[\overrightarrow{B C}, \overrightarrow{B S}]=(50 ; 0 ; 25) \Rightarrow \text { một vécto pháp tuyến của }(S B C) \text { là } \vec{n}_{1}=(2 ; 0 ; 1)\\ &\overrightarrow{A C}=(5 ; 5 ; 0), \overrightarrow{A M}=\left(0 ; \frac{5}{2} ; 5\right)\\ &[\overrightarrow{A C}, \overrightarrow{A M}]=\left(25 ;-25 ; \frac{25}{2}\right) \Rightarrow \mathrm{mô} \mathrm{t}\\ &\text { pháp tuyến của }(A M C) \text { là } \vec{n}_{2}=(2 ;-2 ; 1)\\ &\text { Gọi } \varphi \text { là góc giữa hai mặt phẳng }(A M C) \text { và }(S B C) \text { . }\\ &\cos \varphi=\frac{\left|\vec{n}_{1} \cdot \vec{n}_{2}\right|}{\left|\vec{n}_{1}\right| \cdot\left|\vec{n}_{2}\right|}=\frac{|2 \cdot 2+0 \cdot(-2)+1.1|}{\sqrt{2^{2}+0^{2}+1^{2}} \cdot \sqrt{2^{2}+(-2)^{2}+1^{2}}}=\frac{5}{3 \sqrt{5}}\\ &\text { Suy ra: } \tan \varphi=\sqrt{\frac{1}{\cos ^{2} \varphi}-1}=\sqrt{\frac{1}{\left(\frac{5}{3 \sqrt{5}}\right)^{2}}-1}=\frac{2 \sqrt{5}}{5} \end{aligned}\)