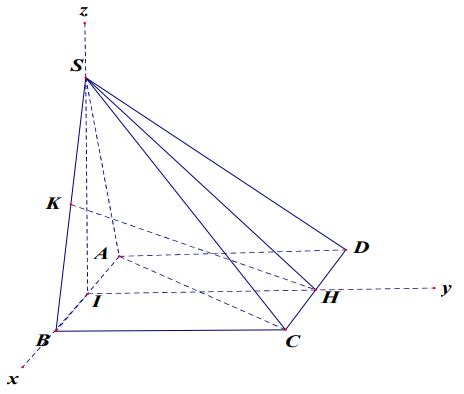
Cho hình chóp S ABCD . có đáy ABCD là hình vuông, tam giác SAB đều. Hình chiếu của S lên mặt phẳng ( ABCD) trùng với trung điểm I của AB . Gọi H, K lần lượt là trung điểm của DC và SB , biết \(S H=\frac{a \sqrt{7}}{2}\) .Tính khoảng cách giữa HK và SC . 

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x – 2y + 2z – 5 = 0\) và hai điểm \(A\left( { – 3;0;1} \right), B\left( {1; – 1;3} \right)\). Trong các đường thẳng đi qua A và song song với \(\left( P \right)\), đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất có phương trình là.

Trong không gian với hệ tọa độ Oxyz , cho hai điểm \(A(-1 ; 0 ; 1), B(1 ; 2 ;-3)\). Đường thẳng AB cắt mặt phẳng tọa độ (Oyz) tại điểm \(M\left(x_{M} ; y_{M} ; z_{M}\right)\). Giá trị của biểu thức \(T=x_{M}+y_{M}+z_{M}\) là 

Cho 2 vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) biết \(\left| \overrightarrow{u} \right|=\sqrt{2};\,\,\,\left| \overrightarrow{v} \right|=3.\) Góc giữa 2 vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) là \({{45}^{o}}\), độ dài vectơ \(\left[ 5\overrightarrow{u},-3\overrightarrow{v} \right]\) là:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm \(M\left( { – 3\,;\,3\,;\, – 3} \right)\) thuộc mặt phẳng \(\left( \alpha \right):2x – 2y + z + 15 = 0\) và mặt cầu \(\left( S \right):{\left( {x – 2} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 5} \right)^2} = 100\). Đường thẳng \(\Delta\) qua M, nằm trên mặt phẳng \(\left( \alpha \right)\) cắt \(\left( S \right)\) tại \(A,\;B\) sao cho độ dài AB lớn nhất. Viết phương trình đường thẳng \(\Delta \).

Trong không gian Oxyz , đường thẳng đi qua điểm A(1; 4;-7) và vuông góc với mặt phẳng \(x+2 y-2 z-3=0\) có phương trình là 

Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với A(1;-3;4); B(-2;-5;-7), C(6;-3;-1). Phương trình đường trung tuyến AM của tam giác là
 

Trong không gian với hệ tọa độ Oxyz , cho đường thẳng \(d: \frac{x-1}{1}=\frac{y}{-1}=\frac{x}{2} \text { và điểm } A(1 ; 6 ; 0) \text { . }\) . Tìm giá trị nhỏ nhất của độ dài MA với \(M \in d ?\)

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x-4y-6z-11 = 0. Toạ độ tâm T của (S) là:

Trong không gian với hệ tọa độ Oxyz, véc-tơ nào dưới đây là một véc-tơ pháp tuyến của mặt phẳng (Oxy)?

Trong không gian với hệ tọa độ Oxyz cho đường thẳng d có phương trình \(d:\frac{{x - 1}}{3} = \frac{{y - 2}}{2} = z - 3\). Véc tơ nào dưới đây là véctơ chỉ phương của đường thẳng d ?

Trong không gian Oxyz , cho ba đường thẳng \(d_{1}: \frac{x-1}{2}=\frac{y}{3}=\frac{z+1}{-1} ; d_{2}: \frac{x+2}{1}=\frac{y-1}{-2}=\frac{z}{2}\);\(d_{3}: \frac{x+3}{-3}=\frac{y-2}{-4}=\frac{z+5}{8}\). Đường thẳng song song với \(d_{3},\, cắt \,d_{1}\, và\,d_{2}\) có phương trình là

Cho 4 điểm \(A\,(1;1;0);\,\,B\,(0;2;1);\,\,C\,(1;0;2);\,\,D\,(1;1;1)\). Tính thể tích tứ diện ABCD.

Trong không gian với hệ tọa độ Oxyz , cho mặt cầu\( ( S ) : x^2 + y^2 + z^2 - 2x + 2 y - 4z - 2 = 0\) .  Tính bán kính  r  của mặt cầu

Trong không gian Oxyz cho đường thẳng d có phương trình chính tắc là \(\frac{{x - 5}}{3} = \frac{{y + 1}}{{ - 4}} = \frac{{z - 6}}{2}\)Véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng d?

Trong không gian, cho tam giác OAB cân ở O có \(O A=O B=5 ; \tan \widehat{A O B}=\frac{4}{3}\) . Điểm C di động trên tia Oz vuông góc (OAB) , gọi H là trực tâm của tam giác ABC . Khi C di động trên tia Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng: 

Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng \(\left( P \right):\,\,x - 2y + 2z + 4 = 0;\,\,\left( Q \right):x - 2y + 2z - 6 = 0\).

Mỗi chuyến xe buýt có sức chứa tối đa là 60 hành khách. Một chuyến xe buýt chở x hành khách thì giá tiền cho mỗi hành khách là  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaabmaabaGaaG % 4maiabgkHiTmaalaaabaGaamiEaaqaaiaaisdacaaIWaaaaaGaayjk % aiaawMcaamaaCaaaleqabaGaaGOmaaaaaaa!3C8A! {\left( {3 - \frac{x}{{40}}} \right)^2}(USD)\) . Khẳng định nào sau đây đúng.

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {1;\;2;\; – 3} \right), B\left( {3;\; – 1;\;1} \right)\). Tìm phương trình chính tắc của đường thẳng đi qua A và B.

Tính tích có hướng của cặp vectơ sau: \(\overrightarrow{a}=\left( 1;3;5 \right);\overrightarrow{b}=\left( 2;-1;3 \right).\)

Trong không gian Oxyz , cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 3}} = \frac{z}{4}\) Đường thẳng d có một vector chỉ
phương là