Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4bGaey4kaSIaamyBaiabgkHiTmaalaaabaGaaGym % aaqaaiaaikdacaWG4bGaey4kaSIaaGymaaaaaaa!4093! y = 2x + m - \frac{1}{{2x + 1}}\) có tâm đối xứng là điểm
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có miền xác định của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiabg2 % da9iabl2riHkaacYfadaGadaqaaiabgkHiTmaalaaabaGaaGymaaqa % aiaaikdaaaaacaGL7bGaayzFaaaaaa!3EB7! D = R\backslash \left\{ { - \frac{1}{2}} \right\}\).
Vì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsisldaWcaaqa % aiaaigdaaeaacaaIYaaaaaqabaGccaWG5bGaeyypa0JaeyOhIukaaa!41DA! \mathop {\lim }\limits_{x \to - \frac{1}{2}} y = \infty \) nên đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaaqaaiaaikdaaaaaaa!3A6B! x = - \frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số đã cho.
Vì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaamWaaeaacaWG5bGaeyOeI0YaaeWaaeaacaaIYaGaamiEai % abgUcaRiaad2gaaiaawIcacaGLPaaaaiaawUfacaGLDbaacqGH9aqp % daWfqaqaaiGacYgacaGGPbGaaiyBaaWcbaGaamiEaiabgkziUkabgU % caRiabg6HiLcqabaGcdaqadaqaaiabgkHiTmaalaaabaGaaGymaaqa % aiaaikdacaWG4bGaey4kaSIaaGymaaaaaiaawIcacaGLPaaacqGH9a % qpcaaIWaaaaa!58E4! \mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {2x + m} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( { - \frac{1}{{2x + 1}}} \right) = 0\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcqGHEisP % aeqaaOWaamWaaeaacaWG5bGaeyOeI0YaaeWaaeaacaaIYaGaamiEai % abgUcaRiaad2gaaiaawIcacaGLPaaaaiaawUfacaGLDbaacqGH9aqp % daWfqaqaaiGacYgacaGGPbGaaiyBaaWcbaGaamiEaiabgkziUkabgk % HiTiabg6HiLcqabaGcdaqadaqaaiabgkHiTmaalaaabaGaaGymaaqa % aiaaikdacaWG4bGaey4kaSIaaGymaaaaaiaawIcacaGLPaaacqGH9a % qpcaaIWaaaaa!58FA! \mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {2x + m} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( { - \frac{1}{{2x + 1}}} \right) = 0\)
Nên đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacQ % dacaWG5bGaeyypa0JaaGOmaiaadIhacqGHRaWkcaWGTbaaaa!3D2C! d:y = 2x + m\) là tiệm cận xiên của đồ thị hàm số đã cho
Như vậy đồ thị nhận giao điểm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaGaeyOeI0YaaSaaaeaacaaIXaaabaGaaGOmaaaacaGG7aGaaGPa % Vlaad2gacqGHsislcaaIXaaacaGLOaGaayzkaaaaaa!3FA3! I\left( { - \frac{1}{2};\,m - 1} \right)\) của hai đường tiệm cận làm tâm đối xứng
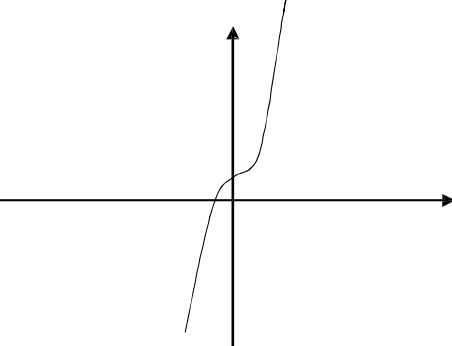
.png)
.png)