Tập các giá trị của m để bất phương trình \(\frac{\log _{2}^{2}x}{\sqrt{\log _{2}^{2}x-1}}\ge m\) nghiệm đúng với mọi x>0 là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=\log _{2}^{2}x\text{ }\left( t>1 \right)\).
Khi đó ta có: \(\frac{t}{\sqrt{t-1}}\ge m\left( * \right)\)
Bất phương trình ban đầu có nghiệm với mọi x>0 \(\Leftrightarrow \left( * \right)\) nghiệm đúng với mọi t>1
Xét hàm số \(f\left( t \right)=\frac{t}{\sqrt{t-1}},\text{ }t\in \left( 1;+\infty \right)\).
\(\begin{align} & f'\left( t \right)=\frac{t-2}{{{\left( \sqrt{t-1} \right)}^{3}}} \\ & f'\left( t \right)=0\Rightarrow t=2 \\ \end{align}\)
\(\underset{x\to \infty }{\mathop{\lim }}\,f\left( t \right)=+\infty ,\text{ }\underset{t\to 1}{\mathop{\lim }}\,f\left( t \right)=+\infty \)
BBT
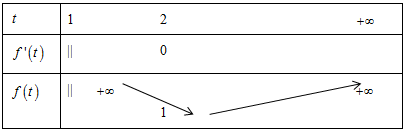
Từ BBT ta có thể kết luận bất phương trình có nghiệm với mọi t > 1 ⇒ \(m \le 1\)











