Tập hợp tất cả các giá trị của tham số thực m để hàm số \(y=\ln \left(x^{2}+1\right)-m x+1\) đồng biến trên khoảng \((-\infty ;+\infty) \text { . }\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\text { Hàm số } y=\ln \left(x^{2}+1\right)-m x+1 \text { có tập xác định } \mathbb{R} \text { . Ta có: } y^{\prime}=\frac{2 x}{x^{2}+1}-m \text { . }\)
\(\text { Hàm số đồng biến trên khoảng }(-\infty ;+\infty) \text { thì } y^{\prime}=\frac{2 x}{x^{2}+1}-m \geq 0, \forall x \in \mathbb{R} \Leftrightarrow m \leq \frac{2 x}{x^{2}+1}, \forall x \in \mathbb{R} \text { . }\)
\(\text { Xét hàm số } g(x)=\frac{2 x}{x^{2}+1} \Rightarrow g^{\prime}(x)=\frac{-2 x^{2}+2}{\left(x^{2}+1\right)^{2}} \text { . }\)
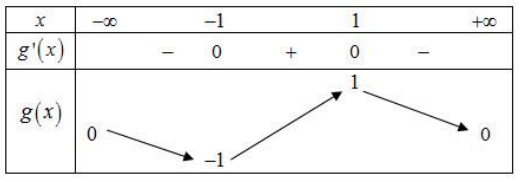
Bảng biến thiên:
\(\text { Từ bảng biến thiên ta suy ra } m \leq-1 \text { thì hàm số đồng biến trên khoảng }(-\infty ;+\infty) \text { . }\)