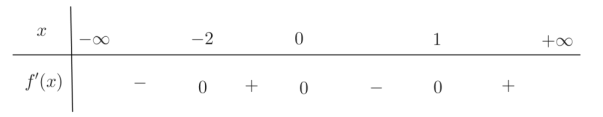Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x+2–2m}{x+m}\) đồng biến trên (–1;2).
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐk: \(x\ne -m\)
Để hàm số đã cho đồng biến trên (–1;2) thì y′>0 với mọi \(x \in(-1 ; 2)\)
\(\Leftrightarrow\left\{\begin{array}{l} m-(2-2 m)>0 \\ -m \notin(-1 ; 2) \end{array} \Leftrightarrow\left\{\begin{array}{l} 3 m-2>0 \\ {\left[\begin{array}{l} m \geq 1 \\ m \leq-2 \end{array} \Leftrightarrow\left\{\left[\begin{array}{l} m>\frac{2}{3} \\ m \geq 1 \end{array} \Leftrightarrow m \geq 1\right.\right.\right.} \\ m \leq-2 \end{array} \Leftrightarrow m \geq 1\right.\right.\)
ADMICRO
YOMEDIA
ZUNIA9
.png)