Xét các số phức z thỏa mãn \(|z-2-3 i|=1\). Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(|\bar{z}+1+i|\)lần lượt là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l} \text { Đặt } z=x+y i \text { vói } x, y \in \mathbb{R} \\ \text { Khi đó }|z-2-3 i|=1 \Leftrightarrow(x-2)^{2}+(y-3)^{2}=1 \end{array}\)
Gọi M là điểm biểu diễn hình học của số phức z ta có \(M \in(I ; 1) \text { với } I(2 ; 3)\)
\(\begin{aligned} &\text { Có }|\bar{z}+1+i|=\sqrt{(x+1)^{2}+(-y+1)^{2}}=\sqrt{(x+1)^{2}+(y-1)^{2}} \text { . }\\ &\text { Gọi } A(-1 ; 1) \text { suy ra }|\bar{z}+1+i|=\sqrt{(x+1)^{2}+(y-1)^{2}}=A M \text { . }\\ &\text { Dễ thấy } A I=\sqrt{13}>1 \text { nên } A \text { nằm ngoài }(I ; 1) \text { . } \end{aligned}\)
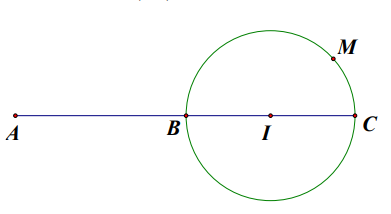
Kẻ đường thẳng AI cắt đường tròn (I;1) tại BC, như hình vẽ.
\(\text { Có } A B \leq A M \leq A C \text { nên }\left\{\begin{array}{l} A M_{\max }=A C=A I+I C=\sqrt{13}+1 \\ A M_{\min }=A B=A I-I B=\sqrt{13}-1 \end{array}\right. \text { . }\)