Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Cho D là miền phẳng giới hạn bởi các đường : \(y=f(x)=\frac{1}{1+x^{2}} ; y=g(x)=\frac{x^{2}}{2}\).Tính thể tích khối tròn xoay thu được tạo thành khi quay D quanh trục Ox ? Thể tích được viết dưới dạng \(T=m \pi^{2}+n \pi ; \mathrm{m}, \mathrm{n} \in \mathrm{R}\) thì tổng giá trị m + n là ?
-
Câu 2:
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y=1-x^{2}, y=0\) quanh trục Ox có kết quả dạng \(\frac{a \pi}{b}\) Khi đó a+b có kết quả là:
-
Câu 3:
Hình phẳng giới hạn bởi hai đồ thị \(y=|x|\text{ và }y=x^{2}\)quay quanh trục tung tạo nên một vật thể tròn xoay có thể tích bằng
-
Câu 4:
Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol \((P): y=x^{2}\) và đường thẳng d: y=2x quay xung quanh trục Ox .
-
Câu 5:
Thể tích khối tròn xoay khi quay hình phẳng (H ) giới hạn bởi\(y=x^{2}\text{ và }y=x+2\) quanh trục Ox là
-
Câu 6:
Cho hình phẳng (H ) giới hạn bởi các đường \(y=x^{2} ; y=0 ; x=2\). Tính thể tích V của khối tròn xoay thu được khi quay (H ) quanh trục Ox .
-
Câu 7:
Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số \( y=x \cdot \ln x\) , trục hoành và hai đường thẳng x =1; x = 2 . Thể tích vật thể tròn xoay sinh bới (H ) khi nó quay quanh trục hoành có thể tích V được xác định bởi
-
Câu 8:
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x \mathrm{e}^{x}, y=0\) , x = 0 , x =1 xung quanh trục Ox là
-
Câu 9:
Cho hình phẳng (D) được giới hạn bởi các đường\(x=0, x=\pi, y=0 \text { và } y=-\sin x.\) Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
. -
Câu 10:
Cho hình phẳng (D) được giới hạn bởi các đường \(x=0, x=1, y=0 \text { và } y=\sqrt{2 x+1}\). Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức?
-
Câu 11:
Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo thành được tính theo công thức nào?
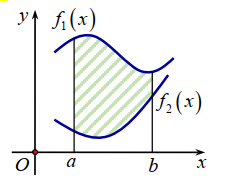
-
Câu 12:
Tính thể tích V của khối tròn xoay tạo thành khi quay hình tròn \(\text { (C ) }:(x+2)^{2}+(y-3)^{2} \leq 1\) quanh trục Ox.
-
Câu 13:
Cho hình phẳng giới hạn bởi đường cong \(y=\tan x\) , trục hoành và hai đường thẳng \(x=0, x=a \text { với } a \in\left(0 ; \frac{\pi}{2}\right)\) Thể tích khối tròn xoay thu được khi quay hình phẳng này xung quanh trục
-
Câu 14:
Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn\((C): x^{2}+(y-3)^{2}=1\) xung quanh trục hoành là
-
Câu 15:
Cho hình phẳng D giới hạn bởi đường cong \(y = e^x\) , trục hoành và các đường thẳng x = 0 , x =1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
-
Câu 16:
Trong hệ trục tọa độ Oxy cho elip (E) có phương trình \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)Hình phẳng (H ) giới hạn bởi nửa elip nằm trên trục hoành và trục hoành. Quay hình (H ) xung quanh trục Ox ta được khối tròn xoay, tính thể tích khối tròn xoay đó:
-
Câu 17:
Cho hình phẳng (H) giới hạn bởi các đường \(y=x^{2}-2 x\) , trục hoành, trục tung, đường thẳng x =1. Tính thể tích V hình tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox.
-
Câu 18:
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường\(y=\sqrt{x}\) , trục Ox và hai đường thẳng x =1; x = 4 khi quay quanh trục hoành được tính bởi công thức nào?
-
Câu 19:
Cho hàm số\(y=\pi^{x}\) có đồ thị (C). Gọi D là hình phẳng giởi hạn bởi (C), trục hoành và hai đường thẳng x = 2 , x = 3. Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính bởi công thức:
-
Câu 20:
Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số \(y=-x^{2}+3 x-2\) , trục hoành và hai đường thẳng x =1, x = 2 . Quay (H ) xung quanh trục hoành được khối tròn xoay có thể tích là:
-
Câu 21:
Cho hàm số y =f(x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox . Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức
.png)
-
Câu 22:
Cho hàm số y=f(x) liên tục trên đoạn [a ;b ]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng \(x=a, x=b(a<b)\) . Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức.
-
Câu 23:
Tích phân \(I=\int_{0}^{1} \frac{1}{x^{2}+1} d x\) có giá trị là:
-
Câu 24:
Tích phân \(I=\int_{\frac{5}{2}}^{3} \sqrt{(x-1)(3-x)} d x\) có giá trị là:
-
Câu 25:
Đổi biến x = 2sint thì tích phân \(\int_{0}^{1} \frac{d x}{\sqrt{4-x^{2}}}\)trở thành:
-
Câu 26:
Giá trị của \(\int_{0}^{3} \sqrt{9-x^{2}} \mathrm{d} x=\frac{a}{b} \pi \text { trong dó } a, b \in \mathbb{Z} \text { và } \frac{a}{b}\). Tính giá trị của biểu thức T=ab
-
Câu 27:
Cho tích phân \(I=\int_{0}^{\frac{1}{2}} \frac{1}{\sqrt{1-x^{2}}} d x=a \pi, a \text { và } b\) là các số hữu tỉ. Giá trị của a là:
-
Câu 28:
Biết rằng \(\int\limits_{-1}^{1} \sqrt{4-x^{2}} \mathrm{d} x=\frac{2 \pi}{3}+a\). Khi đó a bằng:
-
Câu 29:
Khi tính \(I=\int_{0}^{2} \sqrt{4-x^{2}} \mathrm{d} x\) bằng phép đặt \(x=2 \sin t\) thì được
-
Câu 30:
Biết tích phân \(\int\limits_{1}^{2}(4 x-1) \ln x \mathrm{d} x=a \ln 2+b \text { với } a, b \in Z . \text { Tổng } 2 a+b\).
-
Câu 31:
Cho \(\int_{0}^{1} \ln (x+1) \mathrm{d} x=a+\ln b,(a, b \in \mathbb{Z}) . \operatorname{Tính}(a+3)^{b}\)
-
Câu 32:
Cho \(I=\int_{1}^{e} x \ln x \mathrm{d} x=\frac{a \cdot \mathrm{e}^{2}+b}{c} \text { với } a, b, c \in \mathbb{Z}\). Tính T=a+b+c
-
Câu 33:
Biết rằng tích phân \(\int_{0}^{4} \frac{(x+1) e^{x}}{\sqrt{2 x+1}} d x=a e^{4}+b\). Tính \(T=a^{2}-b^{2}\)
-
Câu 34:
Tìm a sao cho \(I=\int_{0}^{a} x \cdot \mathrm{e}^{\frac{x}{2}} d \mathrm{x}=4\), chọn đáp án đúng.
-
Câu 35:
Biết \(I=\int_{0}^{1}(2 x+3) e^{x} \mathrm{d} x=a e+b, \text { với } a, b\) là các số hữu tỉ. Mệnh đề nào sau đây là mệnh đề đúng?
-
Câu 36:
Biết rằng tích phân \(\int_{0}^{1}(2 x+1) e^{x} d x=a+b \cdot e\). Tích a.b bằng:
-
Câu 37:
Cho \(I=\int_{0}^{1} x e^{2 x} \mathrm{d} x=a e^{2}+b(a, b\) là các số hữu tỉ). Khi đó tổng a+b là
-
Câu 38:
Cho \(\int_{0}^{a} x e^{x} \mathrm{d} x=1(a \in \mathbb{R})\). tìm a
-
Câu 39:
Tính \(\int\limits_{0}^{\frac{\pi}{2}}\left(x+\sin ^{2} x\right) \cos x d x\) kết quả là:
-
Câu 40:
Tích phân \(I=\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}} \frac{\left(x^{3}+2 x\right) \cos x+x \cos ^{2} x}{\cos x} d x\) có giá trị là:
-
Câu 41:
Tích phân \(I=\int_{0}^{\frac{\pi}{4}} \frac{2 x-\sin x}{2-2 \cos x} d x\) có giá trị là:
-
Câu 42:
Tích phân \(\int_{0}^{\frac{\pi}{4}} \frac{x}{1+\cos 2 x} \mathrm{d} x=a \pi+b \ln 2, \text { với } a, b\) là các số thực. Tính 16a-8b
-
Câu 43:
Tích phân \(I=\int_{0}^{\frac{\pi}{4}} \frac{x}{1+\cos x} d x\) có giá trị là:
-
Câu 44:
Cho \(I=\int_{0}^{\frac{x}{4}} x \tan ^{2} x d x=\frac{\pi}{a}-\ln \sqrt{b}-\frac{\pi^{2}}{32}\) khi đó tổng a +b bằng
-
Câu 45:
Tính tích phân \(\int_{0}^{\frac{\pi}{3}} \frac{x}{\cos ^{2} x} d x=a \pi+b\). Phần nguyên của tổng a + b là ?
-
Câu 46:
Tính \(\int_{0}^{\pi} x(1+\cos x) d x\) kết quả là:
-
Câu 47:
Cho hàm số \(f(x)=\left\{\begin{array}{lll} 2 x^{2}+x & \text { khi } & x \geq 0 \\ x \cdot \sin x & \text { khi } & x \leq 0 \end{array}\right.\). Tính tích phân \(I=\int_{-\pi}^{1} f(x) \mathrm{d} x\)
-
Câu 48:
Cho số hữu tỷ dương m thỏa mãn \(\int\limits_{0}^{\frac{\pi}{2 m}} x \cdot \cos m x d x=\frac{\pi-2}{2}\).Hỏi số m thuộc khoảng nào trong các khoảng dưới đây?
-
Câu 49:
Tích phân \( \int\limits_{0}^{\pi}(3 x+2) \cos ^{2} x d x\) bằng:
-
Câu 50:
Tính tích phân \(I=\int\limits_{0}^{\pi} x^{2} \cos 2 x \mathrm{d} x\) bằng cách đặt \(\left\{\begin{array}{l} u=x^{2} \\ \mathrm{d} v=\cos 2 x \mathrm{d} x \end{array}\right.\). Mệnh đề nào sau đây đúng?











