Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Biết \(\smallint x{e^{2x}}dx = ax{e^{2x}} + b{e^{2x}} + C\), với a, b ∈ Q. Tính tích a.b
-
Câu 2:
Tính tích phân sau \(G = \mathop \smallint \nolimits_0^{\ln 2} {({e^x} - 1)^2}.{e^x}dx\)
-
Câu 3:
Tính tích phân sau \(F = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \frac{{\sin 2x}}{{1 + {{\sin }^2}x}}dx\)
-
Câu 4:
Tính tích phân sau \(E = \mathop \smallint \nolimits_1^4 \frac{{{e^{\sqrt x }}}}{{\sqrt x }}dx\)
-
Câu 5:
Tính tích phân \(I = \mathop \smallint \nolimits_0^2 \left| {{x^2} - 3x + 2} \right|dx\) ta được kết quả:
-
Câu 6:
Biết \(I = \mathop \smallint \nolimits_0^1 \frac{x}{{4 - {x^2}}}dx = - \frac{1}{2}\ln \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản và a,b>0a,b>0 thì a2−ba2-b bằng
-
Câu 7:
Biết \(\mathop \smallint \nolimits_1^2 \frac{{dx}}{{4{x^2} - 4x + 1}} = \frac{1}{a} - \frac{1}{b}\) thì a và b là nghiệm của phương trình nào sau đây?
-
Câu 8:
Biết \(\mathop \smallint \nolimits_0^3 \frac{{ - x + 8}}{{{x^2} + 5x + 4}}dx = a\ln b - b\ln a\) với a, b > 0 thì \({\left( {\frac{b}{a}} \right)^2}\) bằng:
-
Câu 9:
Tính tích phân sau \(D = \mathop \smallint \nolimits_0^2 \sqrt {4 - {x^2}} xdx\)
-
Câu 10:
Tính tích phân sau \(C = \mathop \smallint \nolimits_1^2 \frac{{{e^x}}}{{{e^x} - 1}}dx\)
-
Câu 11:
Tính tích phân sau \(B = \mathop \smallint \nolimits_0^1 {x^3}{\left( {{x^4} - 1} \right)^5}dx\)
-
Câu 12:
Tính tích phân sau \(A = \mathop \smallint \nolimits_0^1 x\sqrt {1 + {x^2}} dx\)
-
Câu 13:
Tính tích phân sau \(\mathop \smallint \nolimits_1^2 \frac{{{x^2} + 4x}}{x}dx\)
-
Câu 14:
Tính tích phân sau \(\mathop \smallint \nolimits_0^1 \left( {{x^3} - 1} \right)dx\)
-
Câu 15:
Tính \(I = \mathop \smallint \nolimits_0^1 \frac{{2{x^3} + 7{x^2} + 3x - 1}}{{2x + 1}}dx\)
-
Câu 16:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^1 \frac{x}{{4 - {x^2}}}dx\)
-
Câu 17:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^1 \frac{{2x + 9}}{{x + 3}}dx\)
-
Câu 18:
Tính tích phân \(I = \mathop \smallint \nolimits_{ - 2}^2 \left| {{x^2} - 1} \right|dx\) ta được kết quả :
-
Câu 19:
Tính tích phân \(I = \mathop \smallint \nolimits_0^2 \left| {x - 1} \right|dx\) ta được kết quả:
-
Câu 20:
Ta có tích phân \(I = 4\mathop \smallint \nolimits_1^e x\left( {1 + \ln x} \right)dx = a.{e^2} + b.\). Tính M = ab+4(a+b) (trong đó a,b ∈ Z)
-
Câu 21:
Biết rằng \(\mathop \smallint \nolimits_1^2 \ln \left( {x + 1} \right)dx = a\ln 3 + b\ln 2 + c\) với a, b, c là các số nguyên. Tính S = a+b+c.
-
Câu 22:
Kết quả của tích phân \(\mathop \smallint \nolimits_{ - 1}^0 \left( {x + 1 + \frac{2}{{x - 1}}} \right)dx\) được viết dưới dạng \(a+b\ln 2\) với a, b ∈ Q. Khi đó a+b bằng:
-
Câu 23:
Tính thể tích của phần vật thể tạo nên khi quay quanh trục Ox hình phẳng D giới hạn bởi đồ
thị \((P): y=2 x-x^{2}\) -
Câu 24:
Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ
thị\(y=x^{2}-4 x+6 \text { và } y=-x^{2}-2 x+6\) -
Câu 25:
Cho hình phẳng (H ) giới hạn bởi các đường cong \(y=\frac{\ln x}{\sqrt{x}}\), trục hoành và đường thẳng x = e . Khối tròn xoay tạo thành khi quay (H ) quanh trục hoành có thể tích V bằng bao nhiêu?
-
Câu 26:
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(y=\frac{x}{4}, y=0, x=1, x=4\) quay quanh trục Ox bằng
-
Câu 27:
Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y =tan x , trục Ox , đường thẳng x = 0 , đường thẳng \(x=\frac{\pi}{3}\) quanh trục Ox là:
-
Câu 28:
Thể tích của khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x} \mathrm{e}^{x}\), trục hoành và đường thẳng x = 1 là:
-
Câu 29:
Cho hình phẳng D giới hạn bởi đường cong \(y=\sqrt{2+\cos x}\), trục hoành và các đường thẳng\(x=0, x=\frac{\pi}{2}\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?
-
Câu 30:
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số\(y=3 x-x^{2}\) và trục hoành, quanh trục hoành.
-
Câu 31:
Thể tích khối tròn xoay thu được khi quay quanh trục Ox hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{x} \mathrm{e}^{x}\), trục hoành và đường thẳng x=1 là:
-
Câu 32:
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x =1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ \(x(1 \leq x \leq 3)\) thì được thiết diện là hình chữ nhật có hai cạnh là \(3 x \text { và } \sqrt{3 x^{2}-2}\)
-
Câu 33:
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)=x^{2}-4 x+3\), trục hoành và hai đường thẳng \(x=1 ; x=3\). Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành bằng
-
Câu 34:
Xét hình phẳng (H ) giới hạn bởi đồ thị hàm số \(f(x)=a \sin x+b \cos x(\text { vói } a, b\) là các hằng số thực dương), trục hoành, trục tung và đường thẳng \(x=\pi\) . Nếu vật thể tròn xoay được tạo thành khi quay (H ) quanh trục Ox có thể tích bằng\(\frac{5 \pi^{2}}{2} \text { và } f^{\prime}(0)=2 \text { thì } 2 a+5 b\) bằng:
-
Câu 35:
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số\(y=\sqrt{\tan x}\) , trục hoành và các đường thẳng \(x=0, x=\frac{\pi}{4}\) quanh trục hoành là:
-
Câu 36:
Goi (H ) là hình phẳng giới hạn bởi đồ thị hàm số \(y=e^{x}\) , trục Ox và hai đường thẳng x = 0, x =1. Thể tích của khối tròn xoay tạo thành khi quay (H ) xung quanh trục Ox là:
-
Câu 37:
Gọi (H ) là hình phẳng giới hạn bởi các đồ thị hàm số y = tan x , trục hoành và các đường thẳng \(x=0, x=\frac{\pi}{4}\) Quay (H ) xung quanh trục Ox ta được khối tròn xoay có thể tích bằng
-
Câu 38:
Cho hình phẳng D giới hạn bởi đồ thị \(y=(2 x-1) \sqrt{\ln x}\) , trục hoành và đường thẳng x = e . Khi hình phẳng D quay quanh trục hoành được vật thể tròn xoay có thể tích V được tính theo công thức
-
Câu 39:
Cho hình thang cong (H ) giới hạn bởi các đường\(y=\ln (x+1)\) , trục hoành và đường thẳng x=e-1. Tính thể tích khối tròn xoay thu được khi quay hình (H ) quanh trục Ox
-
Câu 40:
Cho hình phẳng (H ) giới hạn bởi các đường \(y=\sqrt{x}-1\), trục hoành và đường thẳng x = 4 . Khối tròn xoay tạo thành khi quay (H ) quanh trục hoành có thể tích V bằng bao nhiêu?
-
Câu 41:
Cho hình (H ) giới hạn bởi các đường\(y=-x^{2}+2 x\) trục hoành. Quay hình phẳng (H ) quanh trục Ox ta được khối tròn xoay có thể tích là:
-
Câu 42:
Tính thể tích V của vật tròn xoay tạo thành khi quay hình phẳng (H ) giới hạn bởi các đường \(y=x^{2} ; y=\sqrt{x}\) quanh trục Ox .
-
Câu 43:
Cho hình phẳng (H ) giới hạn bởi các đường\(y=x^{2}, y=2 x\) . Thể tích của khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox bằng:
-
Câu 44:
Tính thể tích V của vật thể tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường \(y=\frac{1}{x}, y=0, x=1, x=a,(a>1)\) quay xung quanh trục Ox .
-
Câu 45:
Cho hình phẳng (H ) giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\)và các đường thẳng y = 0, x =1, x = 4 . Thể tích V của khối tròn xoay sinh ra khi cho hình phẳng (H ) quay quanh trục Ox .
-
Câu 46:
Tính thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường \(y=x^{2}-4,y=2 x-4, x=0, x=2\) , x = 0 , x = 2 quanh trục Ox.
-
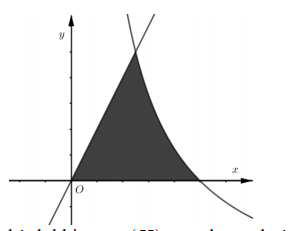
Câu 47:
Gọi (H) là hình phẳng được giới hạn bởi các đồ thị hàm số \(y=2 x, y=\frac{1-x}{x}, y=0\) (phần tô đậm màu đen ở hình vẽ bên).
-
Câu 48:
Cho hình thang cong (H ) giới hạn bởi các đường\(y=\mathrm{e}^{x}, y=0, x=-1, x=1\) Thể tích vật thể tròn xoay được tạo ra khi cho hình (H ) quay quanh trục hoành bằng
-
Câu 49:
Cho hình phẳng (H ) giới hạn bởi các đường \(x y=4, x=0, y=1 \text { và } y=4\). Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H ) quanh trục tung.
-
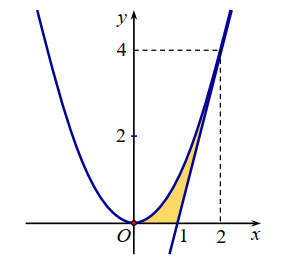
Câu 50:
Cho hình (H ) giới hạn bởi trục hoành, đồ thị của một Parabol và một đường thẳng tiếp xúc với Parabol đó tại điểm A(2;4) , như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình (H ) quay quanh trục Ox bằng: