Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Tính S hình phẳng được giới hạn bởi các đường \(y\; = \;\frac{{{3^x} - 1}}{{\left( {{3^{ - x}} + 1} \right)\sqrt {{3^x} + 1} }}\); y = 0; x = 1
-
Câu 2:
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và \(\mathop \smallint \nolimits_0^2 F\left( x \right)g\left( x \right)dx=3\). Tính tích phân hàm: \(\mathop \smallint \nolimits_0^2 G\left( x \right)f\left( x \right)dx\)
-
Câu 3:
Cho hàm số f(x) thỏa mãn \(\mathop \smallint \nolimits_0^1 \left( {x + 1} \right)f'\left( x \right)dx\; = \;10\) và 2f(1) – f(0) = 2. Tính \(\mathop \smallint \nolimits_0^1 f\left( x \right)dx\)
-
Câu 4:
Cho \(\mathop \smallint \nolimits_1^2 f\left( x \right)dx\; = \; - 3\). Tính \(\mathop \smallint \nolimits_2^4 f\left( {\frac{x}{2}} \right)dx\)
-
Câu 5:
Tính tích phân \(I\; = \;\mathop \smallint \nolimits_1^5 \frac{1}{{x\sqrt {3x\; + \;1} }}dx\) được kết quả I = aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a2 + ab + 3b2 là
-
Câu 6:
Cho m thỏa mãn \(\mathop \smallint \nolimits_1^2 \left[ {{m^2} + \left( {4 - 4m} \right)x\; + 4{x^3}} \right]dx\; = \;\mathop \smallint \nolimits_2^4 2xdx\). Nghiệm của phương trình \({\log _3}\;\left( {x + m} \right)\; = \;1\) là:
-
Câu 7:
Biết \(\mathop \smallint \nolimits_a^b \left( {2x - 1} \right)dx\; = \;1\). Khẳng định nào sau đây đúng?
-
Câu 8:
Cho \(\mathop \smallint \nolimits_1^2 f\left( {{x^2} + 1} \right)xdx\; = \;2\;\). Khi đó \(\mathop \smallint \nolimits_2^5 f\left( x \right)dx\) bằng
-
Câu 9:
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) = 12 và \(\mathop \smallint \nolimits_1^4 f'\left( x \right)dx\; = \;17\) . Giá trị của f(4) bằng
-
Câu 10:
Cho (H) là hình phẳng giới hạn bởi parabol \(y=\sqrt 3 {x^2}\) và nửa đường tròn có phương trình \(y=\sqrt {4\; - {x^2}} \) với −2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
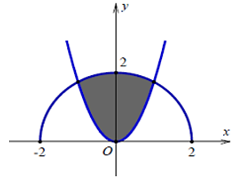
-
Câu 11:
Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bời hai đồ thị y = x2− 4x + 6 và y = −x2−2x + 6
-
Câu 12:
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x, \(x\; = \;\frac{{\rm{\pi }}}{2}\)
-
Câu 13:
Cho hàm số f(x) liên tục trên R và các tích phân \(\mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{4}} f\left( {\tan \;x} \right)dx\) và\(\mathop \smallint \nolimits_0^1 \frac{{{x^2}f\left( x \right)}}{{{x^2} + 1}}dx\), tính tích phân \(\mathop \smallint \nolimits_0^1 f\left( x \right)dx\)
-
Câu 14:
Cho hàm số f(x) liên tục trên R và f(2) = 16, \(\mathop \smallint \nolimits_0^2 f\left( x \right)dx\; = \;4\). Tính \(\mathop \smallint \nolimits_0^1 xf'\left( {2x} \right)dx\)
-
Câu 15:
Diện tích hình phẳng giới hạn bởi các đường thẳng \(y\; = \;\left\{ {\begin{array}{*{20}{l}}
{ - x,x \le 1}\\
{x - 2,\;x > 1}
\end{array}} \right.\) và \(y=\frac{{10}}{3}x\; - \;{x^2}\) là a/b . Khi đó a + 2b bằng -
Câu 16:
Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số \(y\; = \;\frac{{{x^2}}}{4}\) trong miền x ≥ 0, y ≤ 1 là a/b. Khi đó b - a bằng
-
Câu 17:
Cho parabol (P): y = x2+m. Gọi (d) là tiếp tuyến với (P) qua O có hệ số góc k > 0. Xác định m để khi cho Oy quay quanh hình phẳng giới hạn bởi (P), (d) và trục Oy có thể tích bằng 6π.
-
Câu 18:
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = √3 , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục tại điểm có hoành độ x (\(0 \le x \le \sqrt 3 \)) là một hình chữ nhật có độ dài hai cạnh là x và \(\sqrt {1 + {x^2}} \)
-
Câu 19:
Diện tích hình phẳng trong hình vẽ sau là

-
Câu 20:
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = {x^2};\;y = \frac{1}{{27}}{x^2};\;y = \frac{{27}}{x}\) bằng
-
Câu 21:
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \({y^2} - 2y + x = 0,\;x + y = 0\) là
-
Câu 22:
Diện tích hình phẳng giới hạn bởi \(\left( P \right):\;y = {x^2} + 3\), tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung bằng
-
Câu 23:
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y = \left| {{x^2} - 1} \right|,\;y = \left| x \right| + 5\). Diện tích của (H) bằng
-
Câu 24:
Tính thể tích khối tròn xoay khi quay quanh Ox đồ thị hàm số : \(y = \frac{1}{3}{x^3} - {x^2}\) và các đường y = 0, x = 0, x = 3.
-
Câu 25:
Tính thể tích khối tròn xoay khi quay quanh Ox. Đồ thị hàm số y = cosx, y = 0, x = 0 , \(x = \frac{{\rm{\pi }}}{4}\)
-
Câu 26:
Tính thể tích khối tròn xoay khi quay quanh Ox; đồ thị hàm số y = sinx, trục hoành, đường thẳng \(x = \frac{{\rm{\pi }}}{2},\;x = {\rm{\pi }}\)
-
Câu 27:
Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = {e^x};\;y = 2\) và đường thẳng x = 1
-
Câu 28:
Tính diện tích hình phẳng giới hạn bởi :Trục tung, trục hoành và đồ thị hàm số : \(y = \frac{{2x + 1}}{{x + 1}}\)
-
Câu 29:
Diện tích hình phẳng giới hạn bởi các đường \(y = {x^3} + 11x - 6,\;y = 6{x^2}\), x = 0, x = 2. (Đơn vị diện tích)
-
Câu 30:
Nếu \(\mathop \smallint \nolimits_1^2 f\left( x \right)dx = 2\) thì \(I = \mathop \smallint \nolimits_1^2 \left[ {3f\left( x \right) - 2} \right]dx\) bằng bao nhiêu?
-
Câu 31:
Biết rằng \(\smallint {e^{2x}}\cos 3xdx = {e^{2x}}\left( {a\cos 3x + b\sin 3x} \right) + c\) trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là
-
Câu 32:
Cho hàm số y = f(x) xác định trên R, thỏa mãn f(x)>0, ∀x∈R và f’(x) + 2f(x) = 0. Tính f(-1), biết rằng f(1) = 1.
-
Câu 33:
Biết rằng \(\mathop \int \nolimits_0^1 3{e^{\sqrt {1 + 3x} }}dx = \frac{a}{5}{e^2} + \frac{b}{3}e + c\left( {a,b,c, \in Z} \right)\). Tính \(T = a + \frac{b}{2} + \frac{c}{3}\)
-
Câu 34:
Tính tích phân \(I = \mathop \smallint \nolimits_0^2 \left| {{3^x} + x - 4} \right|dx\) ta được kết quả \(I = a + \frac{b}{{\ln c}}\) (với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức \(T = {a^3} + 3{b^2} + 2c\) bằng:
-
Câu 35:
Cho hai số thực a và b thỏa mãn a < b và \(\mathop \smallint \nolimits_a^b x\sin xdx = {\rm{\pi }}\) đồng thời a cos a = 0 và bcosb = −π.Tính tích phân \(\mathop \smallint \nolimits_a^b \cos xdx\)
-
Câu 36:
Tìm tất cả các số hữu tỉ m dương thỏa mãn \(\mathop \smallint \nolimits_0^m \frac{{{x^2}}}{{x + 1}}dx = \ln 2 - \frac{1}{2}\)
-
Câu 37:
Giả sử \(\mathop \smallint \nolimits_0^2 \frac{{x - 1}}{{{x^2} + 4x + 3}}dx = a\ln 5 + b\ln 3;\;a,b \in Q\). Tính P = ab.
-
Câu 38:
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ [0;a], ta có f(x) > 0 và f(x)f(a – x) = 1. Tính \(I = \mathop \smallint \nolimits_0^a \frac{{dx}}{{1 + f\left( x \right)}}\)
-
Câu 39:
Tính tích phân sau \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \frac{{{e^x}.\sin x}}{{1 + \sin 2x}}dx\)
-
Câu 40:
Tính tích phân \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} {\sin ^2}x\cos xdx\)
-
Câu 41:
Cho hàm số f(x) liên tục trên R và có \(\mathop \smallint \nolimits_0^2 f\left( x \right)dx = 3\). Tính \(\mathop \smallint \nolimits_{ - 1}^1 \left| {f\left( {2x} \right)} \right|dx\)
-
Câu 42:
Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) = a, f(2017) = b, \(\left( {a;\;b \in R} \right)\). Giá trị \(I = \mathop \smallint \nolimits_{2017}^{2016} 2015f'\left( x \right).{f^{2014}}\left( x \right)dx\) bằng:
-
Câu 43:
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và \(I = \mathop \smallint \nolimits_0^1 f\left( x \right)dx = 2\). Tính tích phân \(I = \mathop \smallint \nolimits_0^1 f'\left( {\sqrt x } \right)dx\)
-
Câu 44:
Cho tích phân \(I = \mathop \smallint \nolimits_{\frac{1}{2}}^3 \frac{{dx}}{{\left( {x + 1} \right)\sqrt {2x + 3} }}\). Đặt \(t = \sqrt {2x + 3} \) ta được \(I = \mathop \smallint \nolimits_2^3 \frac{m}{{{t^2} + n}}dt\) (với m, n ∈ Z). Tính T = 3m + n
-
Câu 45:
Tính tích phân \(I = \mathop \smallint \nolimits_{ - 1}^0 \left( {2{x^2} + x + 1} \right)\ln \left( {x + 2} \right)dx\)
-
Câu 46:
Tính \(I = \mathop \smallint \nolimits_1^2 \frac{{dx}}{{x{{\left( {x + 1} \right)}^2}}}\)
-
Câu 47:
Tính tích phân: \(I = \mathop \smallint \nolimits_0^2 \left( {x - 2} \right){e^{2x + 1}}dx\)
-
Câu 48:
Tính tích phân: \(I = \mathop \smallint \nolimits_1^3 \frac{{3 + \ln x}}{{{{\left( {x + 1} \right)}^2}}}dx\)
-
Câu 49:
Tính tích phân \(I = \mathop \smallint \nolimits_0^{\sqrt 3 } \frac{{{x^3}}}{{\sqrt {{x^2} + 1} }}dx\)
-
Câu 50:
Tính tích phân \(I = \mathop \smallint \nolimits_0^{\frac{{\sqrt 2 }}{2}} \frac{{{x^2}}}{{\sqrt {1 - {x^2}} }}dx\)











