Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiaaic % dacqGHWcaSaaa!395A! 60^\circ \) . Tính độ dài đường cao SH.
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai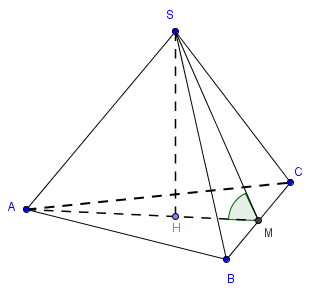
Gọi M là trung điểm của BC
Vì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaamaabmaabaGaam4uaiaadkeacaWGdbaacaGLOaGaayzkaaGaeyyk % IC8aaeWaaeaacaWGbbGaamOqaiaadoeaaiaawIcacaGLPaaacqGH9a % qpcaWGcbGaam4qaaqaaiaadofacaWGnbGaeyOGIW8aaeWaaeaacaWG % tbGaamOqaiaadoeaaiaawIcacaGLPaaacaGG6aGaam4uaiaad2eacq % GHLkIxcaWGcbGaam4qaaqaaiaadgeacaWGnbGaeyOGIW8aaeWaaeaa % caWGbbGaamOqaiaadoeaaiaawIcacaGLPaaacaGG6aGaamyqaiaad2 % eacqGHLkIxcaWGcbGaam4qaaaacaGL7baaaaa!5D5D! \left\{ \begin{array}{l} \left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ SM \subset \left( {SBC} \right):SM \bot BC\\ AM \subset \left( {ABC} \right):AM \bot BC \end{array} \right.\).\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aae % caaeaacaWGtbGaamyqaiaad2eaaiaawkWaaiabg2da9iaaiAdacaaI % WaWaaWbaaSqabeaacaqGVbaaaaaa!3F22! \Rightarrow \widehat {SAM} = {60^{\rm{o}}}\)
Gọi H là trọng tâm tam giác ABC . Vì S.ABC là hình chóp đều nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D27! SH \bot \left( {ABC} \right)\).
Trong tam giác SHM vuông có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpcaWGibGaamytaiaac6caciGG0bGaaiyyaiaac6gacaaI % 2aGaaGimaiabgclaWkabg2da9maalaaabaGaamyyamaakaaabaGaaG % 4maaWcbeaaaOqaaiaaiAdaaaGaaiOlamaakaaabaGaaG4maaWcbeaa % kiabg2da9maalaaabaGaamyyaaqaaiaaikdaaaGaaiOlaaaa!49C2! SH = HM.\tan 60^\circ = \frac{{a\sqrt 3 }}{6}.\sqrt 3 = \frac{a}{2}.\)
Câu hỏi liên quan
-
Cho hàm số \(y=sin2x\) . Khẳng định nào sau đây là đúng?
-
Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t(h) được cho bởi công thức: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2 % da9iaaiodaciGGJbGaai4BaiaacohadaqadaqaamaalaaabaGaeqiW % daNaamiDaaqaaiaaiAdaaaGaey4kaSYaaSaaaeaacqaHapaCaeaaca % aIZaaaaaGaayjkaiaawMcaaiabgUcaRiaaigdacaaIYaaaaa!464B! h = 3\cos \left( {\frac{{\pi t}}{6} + \frac{\pi }{3}} \right) + 12\)
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
-
Tìm hoành độ các giao điểm của đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4bGaeyOeI0YaaSaaaeaacaaIXaGaaG4maaqaaiaa % isdaaaaaaa!3CE3! y = 2x - \frac{{13}}{4}\) với đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % igdaaeaacaWG4bGaey4kaSIaaGOmaaaaaaa!3E3A! y = \frac{{{x^2} - 1}}{{x + 2}}\) .
-
Khẳng định nào sau đây đúng:
-
Đồ thị sau đây là của hàm số nào?
.png)
-
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaa % dIhacqGHRaWkcaaIXaaabaGaeyOeI0IaaGPaVlaaiwdacaWG4bWaaW % baaSqabeaacaaIYaaaaOGaeyOeI0IaaGOmaiaadIhacqGHRaWkcaaI % Zaaaaaaa!46E0 y = \frac{{{x^2} + x + 1}}{{ - \,5{x^2} - 2x + 3}}\) có bao nhiêu đường tiệm cận?
-
Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaaG4maaaakiabg2da9iaaikdacaaIWaGaamOB % aaaa!3C0F! A_n^3 = 20n\) là:
-
Trong mặt phẳng Oxy , tìm phương trình đường tròn (C') là ảnh của đường tròn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadIhadaahaaWcbeqaaiaaikda % aaGccqGHRaWkcaWG5bWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaG % ymaaaa!3F87! \left( C \right):{x^2} + {y^2} = 1\) qua phép đối xứng tâm I( 1; 0) .
-
Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại A , AC =AB= 2a , góc giữa AC' và mặt phẳng (ABC) bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiaaic % dacqGHWcaSaaa!3957! 30^\circ \). Thể tích khối lăng trụ ABC.A'B'C' là
-
Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqOXdOgaaa!37B0! \varphi \) . Thể tích của khối chóp đó bằng
-
Cho lăng trụ đứng tam giác ABC.A'BC' có đáy là một tam giác vuông cân tại B, AB = BC = a,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiqadg % eagaqbaiabg2da9iaadggadaGcaaqaaiaaikdaaSqabaaaaa!3A4F! AA' = a\sqrt 2\) , M là trung điểm BC . Tính khoảng cách giữa hai đường thẳng AM và B'C.
-
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ?
-
Cho hình chóp S.ABC có đáy là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaam % yqaiaadkeacaWGdbaaaa!39AE! \Delta ABC\) vuông cân ở B, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaado % eacqGH9aqpcaWGHbWaaOaaaeaacaaIYaaaleqaaOGaaiilaiaaykW7 % aaa!3C89! AC = a\sqrt 2 ,\,\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadg % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aiaacYcaaaa!3DD0! SA \bot \left( {ABC} \right),\) SA = a. Gọi G là trọng tâm của \(\Delta SBC\) , \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiaadc % hadaqadaqaaiabeg7aHbGaayjkaiaawMcaaaaa!3B02! mp\left( \alpha \right)\) đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V
-
Có bao nhiêu số tự nhiên có sáu chữ số khác nhau từng đôi một, trong đó chữ số 5 đứng liền giữa hai chữ số 1 và 4 ?
-
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích là \(V\), thể tích của khối chóp \(C'.ABC\) là:
-
Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
-
Cho hàm số: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaamiEamaaCaaaleqabaGaaG4maaaaaOqa % aiaaiodaaaGaey4kaSYaaeWaaeaacaWGHbGaeyOeI0IaaGymaaGaay % jkaiaawMcaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkdaqa % daqaaiaadggacqGHRaWkcaaIZaaacaGLOaGaayzkaaGaamiEaiabgk % HiTiaaisdaaaa!4A24! y = - \frac{{{x^3}}}{3} + \left( {a - 1} \right){x^2} + \left( {a + 3} \right)x - 4\) . Tìm a để hàm số đồng biến trên khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIWaGaai4oaiaaykW7caaMc8UaaG4maaGaayjkaiaawMcaaaaa!3CC9! \left( {0;\,\,3} \right)\)
-
Anh Minh muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được \(3200cm^3\) , tỉ số giữa chiều cao và chiều rộng của hố ga bằng 2 . Xác định diện tích đáy của hố ga để khi xây hố tiết kiệm được nguyên vật liệu nhất.
-
Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D28! SH \bot \left( {ABC} \right)\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabgI % GiopaabmaabaGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaaaa!3C23! H \in \left( {ABC} \right)\) . Khẳng định nào sau đây đúng?
-
Chọn kết quả đúng của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaSaaaeaacaaIXaGaey4kaSIaaG4maiaadIhaaeaadaGcaa % qaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4m % aaWcbeaaaaaaaa!4611! \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 3x}}{{\sqrt {2{x^2} + 3} }}\) .
