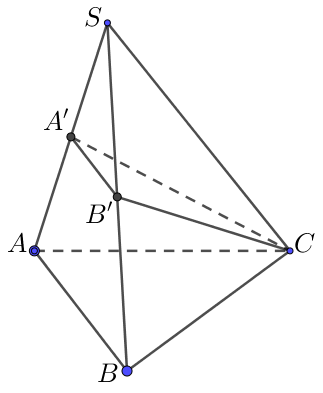
Cho hình chóp \(S.ABC\) có \({A}',\,\,{B}'\) lần lượt là trung điểm của \(SA,\,\,SB\). Mặt phẳng \(\left( C{A}'{B}' \right)\) chia khối chóp thành hai khối đa diện có thể tích lần lượt là \({{V}_{1}},\,\,{{V}_{2}}\) \(\left( {{V}_{1}}>{{V}_{2}} \right)\). Tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\) gần với số nào nhất?

Câu hỏi liên quan

• Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau

  

  Hàm số đã cho đồng biến trên khoảng nào dưới đây?

• Tìm \(a\) để đồ thị hàm số \(y={{\log }_{a}}x\left( 0<a\ne 1 \right)\) có đồ thị là hình bên.

  

• Cho lăng trụ đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a\), góc giữa đường thẳng \(A{B}'\) và mặt phẳng \((BC{B}'{C}')\) bằng \({{30}^{0}}\). Tính thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\).

ZUNIA12

• Tìm tập xác định của hàm số \(y=\ln \left( -{{x}^{2}}+4 \right)\).

• Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a\) cạnh bên bằng \(\frac{3a}{2}\). Góc giữa hai mặt phẳng \(\left( {A}'BC \right)\)và mặt phẳng \(\left( ABC \right)\)bằng

• Trong không gian \(Oxyz\), cho điểm \(M\left( -1;1;3 \right)\) và hai đường thẳng \(\Delta :\frac{x-1}{3}=\frac{y+3}{2}=\frac{z-1}{1}\), \({\Delta }':\frac{x+1}{1}=\frac{y}{3}=\frac{z}{-2}\). Phương trình nào dưới đây là phương trình đường thẳng đi qua \(M\) và vuông góc với \(\Delta \) và \({\Delta }'\).

• Cho hình nón đỉnh \(S,\) đáy là hình tròn tâm \(O,\) góc ở đỉnh của hình nón là \(\varphi =120{}^\circ .\) Cắt hình nón bởi mặt phẳng đi qua đỉnh \(S\) được thiết diện là tam giác vuông \(SAB,\) trong đó \(A,B\) thuộc đường tròn đáy. Biết rằng khoảng cách giữa \(SO\) và \(AB\) bằng \(3.\) Diện tích xung quanh của hình nón bằng

• Trong không gian với hệ tọa độ \(Oxyz\), điểm \(M'\)đối xứng với điểm \(M\left( 2;\,2;\,-1 \right)\)qua mặt phẳng \(\left( Oyz \right)\) có tọa độ là

• Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\frac{x-2}{1}=\frac{y+2}{2}=\frac{z}{-2}\) và mặt phẳng \(\left( P \right):2x-y+2z-2022=0\). Gọi \(\alpha \) là góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\). Khẳng định nào sau đây đúng ?

• Tổng hai nghiệm của phương trình \({{2}^{{{x}^{2}}+x+1}}={{8}^{2x}}\)

• Trên tập hợp các số phức, xét phương trình \({{z}^{2}}-2\left( m+1 \right)z+{{m}^{2}}=0\) (\(m\) là tham số thực). Có bao nhiêu giá trị của \(m\) để phương trình đó có nghiệm \({{z}_{0}}\) thỏa mãn \(\left| {{z}_{0}} \right|=7?\)

• Nghiệm của phương trình \({{2023}^{x-1}}=1\) là

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD=2\sqrt{2},\,\,AB=1,\,\,\)

  \(SA=SB,\,\)\(SC=SD.\) Biết rằng hai mặt phẳng \(\left( SAB \right)\) và \(\left( SCD \right)\) vuông góc với nhau và tổng diện tích của hai tam giác \(SAB\) và \(SCD\) bằng \(\sqrt{3}.\) thể tích của khối chóp \(S.ABCD\) bằng

• Cho đồ thị hàm số \(y=\frac{x}{x-2}\). Khẳng định nào sau đây đúng?

• Cho \(M\) là giao điểm của đồ thị hàm số \(y=\frac{x+1}{x-2}\) với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm \(M\) là

• Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\) có đồ thị là đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right):y=g\left( x \right)\) tiếp xúc với \(\left( C \right)\) tại điểm \({{x}_{0}}=1\). Biết \(\left( d \right)\) và \(\left( C \right)\) còn hai điểm chung khác có hoành độ là \({{x}_{1}},{{x}_{2}}\left( {{x}_{1}}<{{x}_{2}} \right)\) và \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{g\left( x \right)-f\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx=\frac{4}{3}}\). Tính diện tích hình phẳng giới hạn bởi đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right)\).

   

• Số giá trị nguyên của tham số \(m\) để hàm số \(y={{x}^{3}}-3m{{x}^{2}}+3x+1\) đồng biến trên \(\mathbb{R}\) là

• Thể tích khối cầu nội tiếp hình lập phương cạnh \(2a\) là

• Trong không gian với hệ tọa độ \(Oxyz\), vectơ \(\overrightarrow{a}=\left( 1;2;-2 \right)\) vuông góc với vectơ nào sau đây?

• Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.\) Gọi \(A,\,\,B\) là hai điểm trên mặt cầu \(\left( S \right)\) và \(AB=4;\) \({A}',\,\,{B}'\) là hai điểm nằm trên mặt phẳng \(\left( P \right)\) sao cho \(A{A}',\,\,B{B}'\) cùng song song với đường thẳng \(d.\) Giá trị lớn nhất của tổng \(A{A}'+\,B{B}'\) gần nhất với giá trị nào sau đây