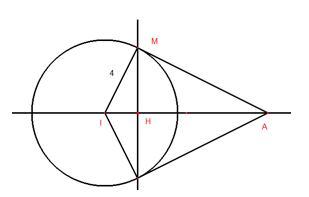
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=16\) và điểm \(A\left( -1;-1;-1 \right).\) Xét các điểm M thuộc \(\left( S \right)\)sao cho đường thẳng AM tiếp xúc với \(\left( S \right).\) M luôn thuộc một mặt phẳng cố định có phương trình là

Câu hỏi liên quan

• Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\), \(\left( a,b,c\in R \right)\) có đồ thị là đường cong như hình bên. Điểm cực tiểu của hàm số đã cho là:

  

• Cho hình nón đỉnh\(S\), đáy là đường tròn \(\left( O;\,5 \right)\).Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm \(A\) và \(B\) sao cho \(SA=AB=8\). Tính khoảng cách từ \(O\) đến \(\left( SAB \right)\).

• Tiệm cận ngang của đồ thị hàm số \(y=\frac{2x-1}{2x+4}\) là đường thẳng có phương trình:

ZUNIA12

• Trong không gian Oxyz, cho điểm \(I\left( 1;-2;3 \right).\) Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho \(AB=2\sqrt{3}.\)

• Số giao điểm của đồ thị \((C):y={{x}^{3}}-3{{x}^{2}}+2x+1\) và đường thẳng \(y=1\) là

• Cho \(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+{{\left( x+\ln x \right)}^{2}}+x}{{{x}^{2}}{{\left( x+\ln x \right)}^{2}}}\text{d}x}=\frac{a}{2}-\frac{1}{b+\ln c}\) với \(a\), \(b\), \(c\) là các số nguyên dương. Khẳng định nào sau đây đúng ?

• Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng \(A{B}'\) và \(C{C}'\) bằng

  

• Cho hình chóp \(S.ABC\)có \(SA=a\) và \(SA\) vuông góc với đáy. Biết đáy là tam giác vuông cân tại \(A\) và \(BC=a\sqrt{2}\). Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( SBC \right)\).

• Cho số phức \(z=-1-2\sqrt{6}i\). Phần thực và phần ảo của số phức \(\overline{z}\) là?

• Tìm mệnh đề đúng trong các mệnh đề sau:

• Tập nghiệm của bất phương trình \({{3}^{{{x}^{2}}-13}}<27\) là

• Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y=\sqrt{3}{{x}^{2}}\), cung tròn có phương trình \(y=\sqrt{4-{{x}^{2}}}\) (với \(0\le x\le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) là

• Nghiệm của phương trình \({{\log }_{3}}\left( 2x+1 \right)=1+{{\log }_{3}}\left( x-1 \right)\) là

• Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\text{ }\!\![\!\!\text{ }-1;\,2]\) và \(f\left( -1 \right)=2023,\,f\left( 2 \right)=-1. \)Tích phân \(\int\limits_{-1}^{2}{{f}'\left( x \right)\text{d}x}\)bằng:

• Đặt \(a={{\log }_{2}}5,\,b={{\log }_{3}}5\). Hãy biểu diễn \({{\log }_{6}}5\)theo \(a\) và \(b\).

• Cho hàm số \(f\left( x \right)\) có đạo hàm\(f'\left( x \right)=x\left( x-1 \right){{\left( x+4 \right)}^{2023}},\,\forall x\in \mathbb{R}\) . Số điểm cực trị của hàm số đã cho là

• Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: \(y={{x}^{3}}-3x\), \(y=x\). Tính S.=

• Đạo hàm của hàm số \(y={{8}^{x}}\) là

• Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ -1;1 \right\}\), thỏa mãn \(f'\left( x \right)=\frac{2}{{{x}^{2}}-1};\ f\left( -3 \right)+f\left( 3 \right)=2\ln 2\) và \(f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=0\). Giá trị của biểu thức \(P=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)\) là:

• Cho hàm số \(f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ -2;5 \right]\) của tham số \(m\) để phương trình \(f\left( x \right)=m\) có đúng hai nghiệm phân biệt?