Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai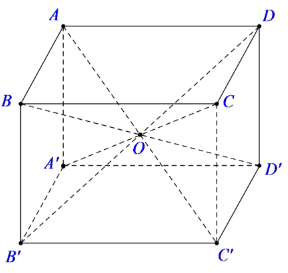
Dễ thấy tâm O của mặt cầu chính là tâm của hình lập phương.
Ta tính OA – bán kính mặt cầu.
Trong tam giác vuông ABC có: AC2 = AB2 + BC2 = 200.
Trong tam giác vuông AA'C có:
\(\begin{array}{l}
A'{C^2} = AA{'^2} + A{C^2} = {10^2} + 200 = 300\\
\Rightarrow A'C = 10\sqrt 3 \left( {cm} \right)
\end{array}\)
Bán kính mặt cầu tâm O là:
\(R = OA' = \frac{1}{2}A'C = 5\sqrt 3 \left( {cm} \right)\)
Diện tích mặt cầu:
\(R = OA' = \frac{1}{2}A'C = 5\sqrt 3 \left( {cm} \right)\)
ADMICRO
YOMEDIA
ZUNIA9











