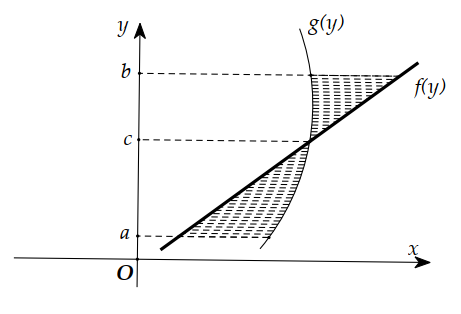
Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned}
&(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và }
\text { (d): } y=4
\end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét phương trình hoành độ giao điểm của (P) và (d):
\(x^{2}=4 \Leftrightarrow\left[\begin{array}{l} x=2 \\ x=-2 \end{array}\right.\)
Xét phương trình hoành độ giao điểm của (P’) và (d):
\(4 x^{2}=4 \Leftrightarrow\left[\begin{array}{l} x=1 \\ x=-1 \end{array}\right.\)
Đặt V là thể tích cần tìm.
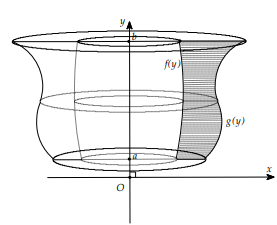
VOAC là thể tích khối tròn xoay sinh bởi khi quay (H'): \(\left\{\begin{array}{l} y=x^{2} \\ y=4 \\ O y \end{array}\right.\) quanh Ox.
VOAB là thể tích khối tròn xoay sinh bởi khi quay (H''): \(\left\{\begin{array}{l}
y=4 x^{2} \\
y=4 \\
O y
\end{array}\right.\) quanh Ox.
Khi đó
\(\begin{aligned} V=V_{O A C}-V_{O A B} &=\pi \int_{0}^{2}\left[4-\left(x^{2}\right)^{2}\right] \mathrm{d} x-\pi \int_{0}^{2}\left[4-\left(4 x^{2}\right)^{2}\right] \mathrm{d} x=\pi \int_{0}^{2}\left(4-x^{4}\right) \mathrm{d} x-\pi \int_{0}^{1}\left(4-16 x^{4}\right) \mathrm{d} x \\ &=\left.\pi\left(4 x-\frac{x^{5}}{5}\right)\right|_{0} ^{2}-\left.\pi\left(4 x-16 \cdot \frac{x^{5}}{5}\right)\right|_{0} ^{1}=\pi\left(8-\frac{32}{5}-4+\frac{16}{5}\right)=\frac{4 \pi}{5}(\text { d.v.t.t }) \end{aligned}\)

.PNG)