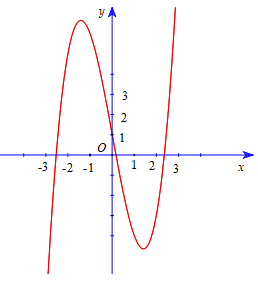
Biết đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaIZaGaamiE % aiabgUcaRiaaigdaaaa!3E2D! y = {x^3} - 3x + 1\) có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiThực hiện phép chia y cho y' ta được: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iqadMhagaqbaiaac6cadaqadaqaamaalaaabaGaaGymaaqaaiaa % iodaaaGaamiEaaGaayjkaiaawMcaaiabgUcaRmaabmaabaGaeyOeI0 % IaaGOmaiaadIhacqGHRaWkcaaIXaaacaGLOaGaayzkaaaaaa!4470! y = y'.\left( {\frac{1}{3}x} \right) + \left( { - 2x + 1} \right)\)
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaaIXaaabeaakiaacUdacaWG5bWaaSba % aSqaaiaaigdaaeqaaaGccaGLOaGaayzkaaaaaa!3CDF! A\left( {{x_1};{y_1}} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaaIYaaabeaakiaacUdacaWG5bWaaSba % aSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaaaaa!3CE2! B\left( {{x_2};{y_2}} \right)\).
Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadMhadaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaWG5bWaaeWa % aeaacaWG4bWaaSbaaSqaaiaaigdaaeqaaaGccaGLOaGaayzkaaGaey % ypa0JabmyEayaafaWaaeWaaeaacaWG4bWaaSbaaSqaaiaaigdaaeqa % aaGccaGLOaGaayzkaaGaaiOlamaabmaabaWaaSaaaeaacaaIXaaaba % GaaG4maaaacaWG4bWaaSbaaSqaaiaaigdaaeqaaaGccaGLOaGaayzk % aaGaey4kaSYaaeWaaeaacqGHsislcaaIYaGaamiEamaaBaaaleaaca % aIXaaabeaakiabgUcaRiaaigdaaiaawIcacaGLPaaacqGH9aqpcqGH % sislcaaIYaGaamiEamaaBaaaleaacaaIXaaabeaakiabgUcaRiaaig % daaeaacaWG5bWaaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaamyEamaa % bmaabaGaamiEamaaBaaaleaacaaIYaaabeaaaOGaayjkaiaawMcaai % abg2da9iqadMhagaqbamaabmaabaGaamiEamaaBaaaleaacaaIYaaa % beaaaOGaayjkaiaawMcaaiaac6cadaqadaqaamaalaaabaGaaGymaa % qaaiaaiodaaaGaamiEamaaBaaaleaacaaIYaaabeaaaOGaayjkaiaa % wMcaaiabgUcaRmaabmaabaGaeyOeI0IaaGOmaiaadIhadaWgaaWcba % GaaGOmaaqabaGccqGHRaWkcaaIXaaacaGLOaGaayzkaaGaeyypa0Ja % eyOeI0IaaGOmaiaadIhadaWgaaWcbaGaaGOmaaqabaGccqGHRaWkca % aIXaaaaiaawUhaaaaa!7810! \left\{ \begin{array}{l} {y_1} = y\left( {{x_1}} \right) = y'\left( {{x_1}} \right).\left( {\frac{1}{3}{x_1}} \right) + \left( { - 2{x_1} + 1} \right) = - 2{x_1} + 1\\ {y_2} = y\left( {{x_2}} \right) = y'\left( {{x_2}} \right).\left( {\frac{1}{3}{x_2}} \right) + \left( { - 2{x_2} + 1} \right) = - 2{x_2} + 1 \end{array} \right.\)
Ta thấy, toạ độ hai điểm cực trị A và B thoả mãn phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdacaWG4bGaey4kaSIaaGymaaaa!3C3B! y = - 2x + 1\)
Vậy phương trình đường thẳng qua hai điểm cực trị là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdacaWG4bGaey4kaSIaaGymaaaa!3C3B! y = - 2x + 1\)
Câu hỏi liên quan
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + ax + b\) có điểm cực tiểu A(2;−2). Tìm tổng (a+b)
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3 \sqrt{x-1}+m \sqrt{x+1}=2 \sqrt[4]{x^{2}-1}\) có hai nghiệm thực?
-
Đồ thị ở hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
-
Tất cả giá trị của tham số m để đồ thị \((C): y=x^{4}-2 x^{2}-3\) cắt đường thẳng d: y=m tại bốn điểm phân biệt là
-
Cho hàm số \(f(x)=x^{4}-4 x^{2}+3\) có đồ thị là đường cong trong hình bên. Hỏi phương trình \(\left(x^{4}-4 x^{2}+3\right)^{4}-4\left(x^{4}-4 x^{2}+3\right)^{2}+3=0\) có bao nhiêu nghiệm thực phân biệt ?
8 -
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\)và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=|f(x)|?
.png)
-
Đường cong trong hình bên là đồ thị của hàm số nào sau đây?
-
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x)-1
.png)
-
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
-
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm:\(\sqrt{x+5}+\sqrt{4-x} \geq m\)
-
Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiwdaaaa!3F2E! y = {x^4} - 3{x^2} - 5\) có đồ thị (C). Điểm nào sau đây thuộc đồ thị (C)?
-
A,B là hai điểm di động và thuộc hai nhánh khác nhau của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHsislcaaIXaaabaGaamiEaiab % gUcaRiaaikdaaaaaaa!3E04! y = \frac{{2x - 1}}{{x + 2}}\). Khi đó khoảng cách AB bé nhất là?
-
Tất cả giá trị của tham số m để phương trình \(x^{4}-2 x^{2}-m+3=0\) có hai nghiệm phân biệt là
-
Tọa độ giao điểm giữa đồ thị \((C):y = \frac{{2x – 1}}{{x + 2}}\) và đường thẳng \(d:y = x – 2\) là
-
Tính tổng các hoành độ của những điểm thuộc đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadMhacqGH9aqpcaWG4bWaaWba % aSqabeaacaaIZaaaaOGaeyOeI0IaaG4maiaadIhadaahaaWcbeqaai % aaikdaaaGccqGHRaWkcaaIYaaaaa!4230! \left( C \right):y = {x^3} - 3{x^2} + 2\) cách đều hai điểm A(12;1),B(-6;3) .
-
Một con cá hồi bơi ngược để vượt một khoảng cách là 500km. Vận tốc của dòng nước là 5km/h. Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức E(v)=cv3t. Trong đó, c là một hằng số, E được tính bằng jun. Vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao ít nhất là
-
Đồ thị hàm số \(y = \frac{{2x + 3}}{{x + 3}}\) cắt trục tung tại điểm có tung độ bằng
-
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?
-
Giá trị của m để phương trình \(x+\sqrt{2 x^{2}+1}=m\) có nghiệm là:
