Tìm m để bất phương trình \(m{.9^x} – (2m + 1){.6^x} + m{.4^x} \le 0\) nghiệm đúng với mọi \(x \in \left( {0;1} \right)\).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(m{.9^x} – \left( {2m + 1} \right){.6^x} + m{.4^x} \le 0 \Leftrightarrow m.{\left( {\frac{9}{4}} \right)^x} – \left( {2m + 1} \right){\left( {\frac{3}{2}} \right)^x} + m \le 0\).
Đặt \(t = {\left( {\frac{3}{2}} \right)^x}\). Vì \(x \in \left( {0;1} \right)\) nên \(1 < t < \frac{3}{2}\)
Khi đó bất phương trình trở thành \(m.{t^2} – \left( {2m + 1} \right)t + m \le 0 \Leftrightarrow m \le \frac{t}{{{{\left( {t – 1} \right)}^2}}}\)
Đặt \(f\left( t \right) = \frac{t}{{{{\left( {t – 1} \right)}^2}}}\).
Ta có \(f’\left( t \right) = \frac{{ – t – 1}}{{{{\left( {t – 1} \right)}^3}}}, f’\left( t \right) = 0 \Leftrightarrow t = – 1\).
Bảng biến thiên.
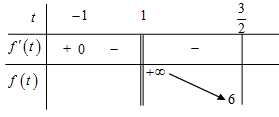
Dựa vào bảng biến thiên ta có \(m \le \mathop {\lim }\limits_{t \to \frac{3}{2}} f\left( t \right) = 6\).











