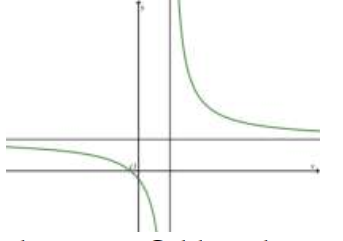
Tìm tất cả các đường tiệm cận của đồ thị hàm số \(y=\frac{x+3}{\sqrt{x^{2}+1}}\)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiVì TXĐ của hàm số là R nên đồ thị hàm số không có tiệm cận đứng
Lại có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 3}}{{\sqrt {{x^2} + 1} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \frac{3}{x}}}{{\sqrt {1 + \frac{1}{{{x^2}}}} }} = 1{\rm{ và }}\mathop {\lim }\limits_{x \to - \infty } \frac{{x + 3}}{{\sqrt {{x^2} + 1} }} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 + \frac{3}{x}}}{{ - \sqrt {1 + \frac{1}{{{x^2}}}} }} = - 1\)Vậy đồ thị hàm số có hai đường tiệm cận ngang là \(y=\pm 1\)
ADMICRO
YOMEDIA
ZUNIA9

.png)