Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐiều kiện: ≥ -1/2
Phương trình
Vì x = 0 không là nghiệm nên (*)
\( \Leftrightarrow m = \frac{{3{x^2} + 4x - 1}}{x}\)
Xét \(f\left( x \right) = \frac{{3{x^2} + 4x - 1}}{x}\)
Ta có đạo hàm
\(f'\left( x \right) = \frac{{3{x^2} + 1}}{{{x^2}}} > 0,\forall x \ge - \frac{1}{2};x \ne 0\)
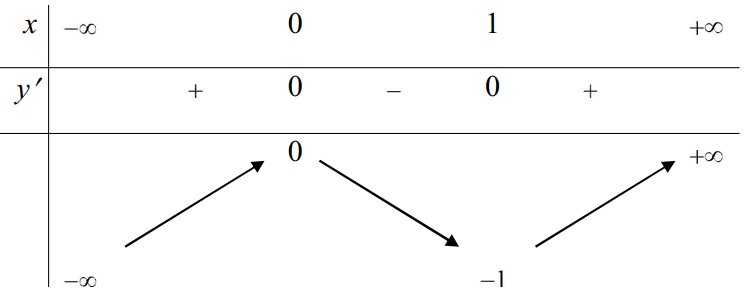
Bảng biến thiên
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9/2.
ADMICRO
YOMEDIA
ZUNIA9