Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(\sqrt 2 a\). Tam giác SAD cân tại \(S\) và mặt bên \(\left( {SAD} \right)\) vuông góc với mp đáy. Biết thể tích khối chóp S.ABCD bằng \(\dfrac{4}{3}{a^3}\). Tính khoảng cách h từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\)?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai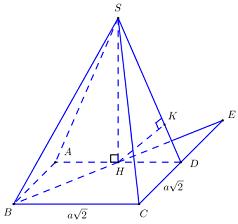
Kẻ \(SH \bot AD \Rightarrow H\) là trung điểm của AD\((\)\Delta SAD cân tại \(S\)).
Kéo dài \(BH \cap CD = E\).
\(\left\{ {\begin{array}{*{20}{l}}{\left( {SAD} \right) \bot \left( {ABCD} \right)}\\{SH \supset \left( {SAD} \right)}\end{array}} \right. \Rightarrow SH \bot \left( {ABCD} \right)\).
Xét tam giác EBC có: \(\left\{ {\begin{array}{*{20}{l}}{HD\parallel BC}\\{HD = \dfrac{1}{2}BC}\end{array}} \right. \Rightarrow HD\) là đường trung bình của tam giác EBC.
\( \Rightarrow H\) là trung điểm của BE.
\({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} \Leftrightarrow \dfrac{4}{3}{a^3} = \dfrac{1}{3}SH.2{a^2} \Leftrightarrow SH = 2a\).
Kẻ \(HK \bot SD \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HK\).
Có \(\dfrac{{d\left( {H;\left( {SCD} \right)} \right)}}{{d\left( {B;\left( {SCD} \right)} \right)}} = \dfrac{{HE}}{{BE}} = \dfrac{1}{2}\).
Xét tam giác SHD vuông tại \(H\) có: \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{S{D^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{\dfrac{{{a^2}}}{2}}} = \dfrac{9}{{4{a^2}}} \Rightarrow HK = \dfrac{{2a}}{3}\).
\(d\left( {B;\left( {SCD} \right)} \right) = 2d\left( {H;\left( {SCD} \right)} \right) = 2HK = 2\dfrac{{2a}}{3} = \dfrac{{4a}}{3}\).
Chọn B.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Lạc Long Quân