Cho tứ diện đều \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadk % eacaWGdbGaamiraaaa!3912! ABCD\) , \(M\) là trung điểm của cạnh \(BC\) . Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaacaWGbbGaamOqaiaacYcacaWGebGaamytaaGa % ayjkaiaawMcaaaaa!3E28! \cos \left( {AB,DM} \right)\) bằng:
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai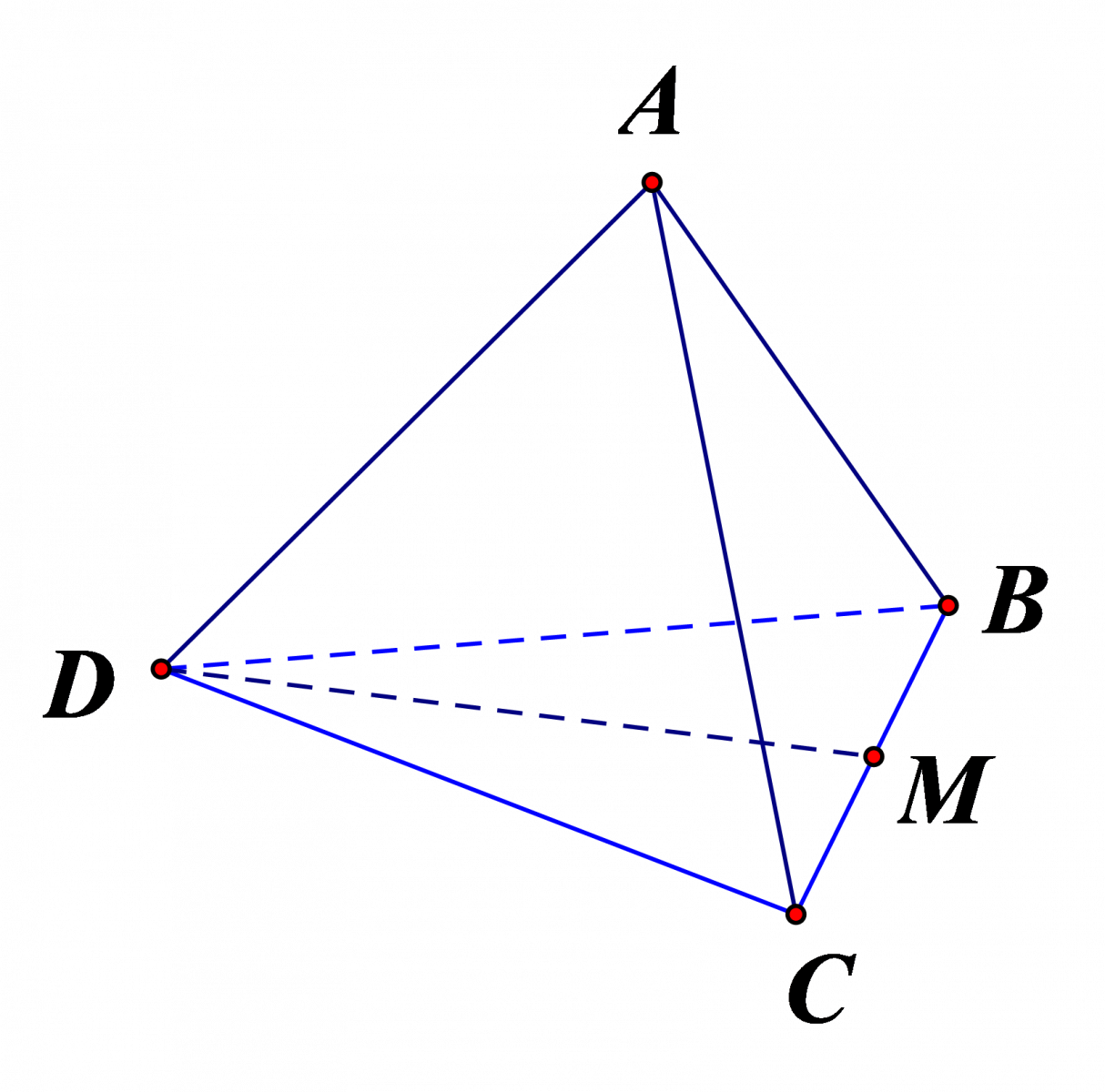
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\) ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiaad2 % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIYaaaaaaa!3B29! DM = \frac{{a\sqrt 3 }}{2}\).
Ta lại có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGG % SaWaa8HaaeaacaWGebGaamytaaGaay51GaaacaGLOaGaayzkaaGaey % ypa0ZaaSaaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGGUaWa % a8HaaeaacaWGebGaamytaaGaay51GaaabaWaaqWaaeaadaWhcaqaai % aadgeacaWGcbaacaGLxdcaaiaawEa7caGLiWoacaGGUaWaaqWaaeaa % daWhcaqaaiaadseacaWGnbaacaGLxdcaaiaawEa7caGLiWoaaaaaaa!576E! \cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGGUaWaa8Haaeaa % caWGebGaamOqaaGaay51GaGaey4kaSYaa8HaaeaacaWGbbGaamOqaa % Gaay51GaGaaiOlamaaFiaabaGaamOqaiaad2eaaiaawEniaaqaaiaa % dggacaGGUaWaaSaaaeaacaWGHbWaaOaaaeaacaaIZaaaleqaaaGcba % GaaGOmaaaaaaaaaa!4A8F! = \frac{{\overrightarrow {AB} .\overrightarrow {DB} + \overrightarrow {AB} .\overrightarrow {BM} }}{{a.\frac{{a\sqrt 3 }}{2}}}\)
.\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaacaWGHbGaaiOlaiaadggacaGGUaGaci4yaiaac+gacaGGZbGa % aGOnaiaaicdacqGHWcaScqGHRaWkcaWGHbGaaiOlamaalaaabaGaam % yyaaqaaiaaikdaaaGaaiOlaiGacogacaGGVbGaai4CaiaaigdacaaI % YaGaaGimaiabgclaWcqaaiaadggacaGGUaWaaSaaaeaacaWGHbWaaO % aaaeaacaaIZaaaleqaaaGcbaGaaGOmaaaaaaaaaa!506D! = \frac{{a.a.\cos 60^\circ + a.\frac{a}{2}.\cos 120^\circ }}{{a.\frac{{a\sqrt 3 }}{2}}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaadaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaaI % 0aaaaaqaaiaadggacaGGUaWaaSaaaeaacaWGHbWaaOaaaeaacaaIZa % aaleqaaaGcbaGaaGOmaaaaaaGaeyypa0ZaaSaaaeaadaGcaaqaaiaa % iodaaSqabaaakeaacaaI2aaaaaaa!4095! = \frac{{\frac{{{a^2}}}{4}}}{{a.\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{6}\)
Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaacaWGbbGaamOqaiaacYcacaWGebGaamytaaGa % ayjkaiaawMcaaiabg2da9maalaaabaWaaOaaaeaacaaIZaaaleqaaa % GcbaGaaGOnaaaaaaa!40E0! \cos \left( {AB,DM} \right) = \frac{{\sqrt 3 }}{6}\)
Câu hỏi liên quan
-
Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaaG4maaaakiabg2da9iaaikdacaaIWaGaamOB % aaaa!3C0F! A_n^3 = 20n\) là:
-
Trong mặt phẳng Oxy , tìm phương trình đường tròn (C') là ảnh của đường tròn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadIhadaahaaWcbeqaaiaaikda % aaGccqGHRaWkcaWG5bWaaWbaaSqabeaacaaIYaaaaOGaeyypa0JaaG % ymaaaa!3F87! \left( C \right):{x^2} + {y^2} = 1\) qua phép đối xứng tâm I( 1; 0) .
-
Tìm giá trị nhỏ nhất của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaaGymaiab % gkHiTiaadIhaaaaaaa!3E03! y = \frac{{2x + 1}}{{1 - x}}\) trên đoạn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaaca % aIYaGaai4oaiaaiodaaiaawUfacaGLDbaaaaa!3A1D! \left[ {2;3} \right]\) .
-
Trong khai triển \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaey4kaSYaaSaaaeaacaaIYaaabaWaaOqaaeaacaWG4baaleaa % aaaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaI2aaaaaaa!3C37! {\left( {x + \frac{2}{{\sqrt[{}]{x}}}} \right)^6}\), hệ số của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaG4maaaakiaacYcaaaa!3895! {x^3},\) \((x>0)\) là:
-
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích là \(V\), thể tích của khối chóp \(C'.ABC\) là:
-
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ?
-
Cho khối chóp S.ABC , trên ba cạnh SA,SB, SC lần lượt lấy ba điểm A' ,B' ,C' sao cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqadg % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaikdaaaGaam4uaiaa % dgeaaaa!3BC8! SA' = \frac{1}{2}SA\) ,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqadk % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaiodaaaGaam4uaiaa % dkeaaaa!3BCB! SB' = \frac{1}{3}SB\) ,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiqado % eagaqbaiabg2da9maalaaabaGaaGymaaqaaiaaisdaaaGaam4uaiaa % doeaaaa!3BCE! SC' = \frac{1}{4}SC\) . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C' . Khi đó tỉ số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaace % WGwbGbauaaaeaacaWGwbaaaaaa!37C5! \frac{{V'}}{V}\) là:
-
Tìm m để phương trình sau có nghiệm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaada % GcaaqaaiaaisdacqGHsislcaWG4baaleqaaOGaey4kaSYaaOaaaeaa % caaI0aGaey4kaSIaamiEaaWcbeaaaOGaayjkaiaawMcaamaaCaaale % qabaGaaG4maaaakiabgkHiTiaaiAdadaGcaaqaaiaaigdacaaI2aGa % eyOeI0IaamiEamaaCaaaleqabaGaaGOmaaaaaeqaaOGaey4kaSIaaG % Omaiaad2gacqGHRaWkcaaIXaGaeyypa0JaaGimaiaac6caaaa!4B96! {\left( {\sqrt {4 - x} + \sqrt {4 + x} } \right)^3} - 6\sqrt {16 - {x^2}} + 2m + 1 = 0.\)
-
Chọn kết quả đúng của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaSaaaeaacaaIXaGaey4kaSIaaG4maiaadIhaaeaadaGcaa % qaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4m % aaWcbeaaaaaaaa!4611! \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 3x}}{{\sqrt {2{x^2} + 3} }}\) .
-
Tìm hoành độ các giao điểm của đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4bGaeyOeI0YaaSaaaeaacaaIXaGaaG4maaqaaiaa % isdaaaaaaa!3CE3! y = 2x - \frac{{13}}{4}\) với đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % igdaaeaacaWG4bGaey4kaSIaaGOmaaaaaaa!3E3A! y = \frac{{{x^2} - 1}}{{x + 2}}\) .
-
Cho hàm số:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaad2gaaiaawIcacaGLPaaacaWG % 4bWaaWbaaSqabeaacaaI0aaaaOGaeyOeI0IaamyBaiaadIhadaahaa % WcbeqaaiaaikdaaaGccqGHRaWkcaaIYaGaamyBaiabgkHiTiaaigda % aaa!4614! y = \left( {1 - m} \right){x^4} - m{x^2} + 2m - 1\) . Tìm m để đồ thị hàm số có đúng một cực trị
-
Tính giới hạn: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaacM % gacaGGTbWaamWaaeaadaqadaqaaiaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawM % caamaabmaabaGaaGymaiabgkHiTmaalaaabaGaaGymaaqaaiaaioda % daahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaaiOlaiaac6 % cacaGGUaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaabaGa % amOBamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaaaiaawU % facaGLDbaaaaa!4E05! \lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)} \right]\) .
-
Khẳng định nào sau đây đúng:
-
Hệ số góc của tiếp tuyến của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaayk % W7cqGH9aqpcaaMc8+aaSaaaeaacaWG4bWaaWbaaSqabeaacaaI0aaa % aaGcbaGaaGinaaaacaaMc8UaaGPaVlabgUcaRiaaykW7daWcaaqaai % aadIhadaahaaWcbeqaaiaaikdaaaaakeaacaaIYaaaaiaaykW7cqGH % sislcaaIXaGaaGPaVdaa!4ACA! y\, = \,\frac{{{x^4}}}{4}\,\, + \,\frac{{{x^2}}}{2}\, - 1\,\)tại điểm có hoành độ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWG4bWdamaaBaaaleaapeGaaGimaaWdaeqaaOGaeyypa0Zdbiab % gkHiTiaaigdaaaa!3AEC! {x_0} = - 1\) bằng :
-
Công thức tính số tổ hợp là:
-
Đồ thị sau đây là của hàm số nào?
.png)
-
Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiaaic % dacqGHWcaSaaa!395A! 60^\circ \) . Tính độ dài đường cao SH.
-
Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là:
-
Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
-
Số mặt phẳng đối xứng của hình lập phương là:
