Đề thi HK1 môn Toán 8 năm 2022-2023
Trường THCS Nguyễn Huệ
-
Câu 1:
Kết quả của phép tính là
A.
B.
C.
D.
-
Câu 2:
Biểu thức bằng:
A.
B.
C.
D.
-
Câu 3:
Phân tích đa thức ta được
A.
B.
C.
D.
-
Câu 4:
Tổng của hai phân thức là
A.
B.
C.
D.
-
Câu 5:
Hình nào sau đây không có tâm đối xứng?
A. Hình bình hành
B. Hình chữ nhật
C. Hình thang cân
D. Cả ba hình trên
-
Câu 6:
Hình thang cân là:
A. Hình thang có hai góc kề một đáy bằng nhau
B. Tứ giác có các cạnh đối song song
C. Hình thang có hai cạnh bên bằng nhau
D. Hình thang có hai đường chéo bằng nhau
-
Câu 7:
Cho tam giác vuông như hình vẽ:
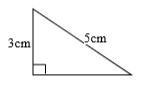
Diện tích của tam giác bằng:
A.
B.
C.
D.
-
Câu 8:
Tìm kết quả phép tính:
A.
B.
C.
D.
-
Câu 9:
Tìm biết:
A.
B.
C.
D. hoặc
-
Câu 10:
Phân tích đa thức sau thành nhân tử: .
A.
B.
C.
D.
-
Câu 11:
Tìm giá trị nhỏ nhất của với mọi số thực .
A. đạt giá trị nhỏ nhất là . Đẳng thức xảy ra khi , hay .
B. đạt giá trị nhỏ nhất là . Đẳng thức xảy ra khi , hay .
C. đạt giá trị nhỏ nhất là . Đẳng thức xảy ra khi , hay .
D. đạt giá trị nhỏ nhất là . Đẳng thức xảy ra khi , hay .
-
Câu 12:
Tìm giá trị nguyên của để .
A. .
B. .
C. .
D. .
-
Câu 13:
Phép nhân được kết quả là
A.
B.
C.
D.
-
Câu 14:
Thực hiện phép chia ta được kết quả là
A.
B.
C.
D.
-
Câu 15:
Chọn câu phát biểu sai?
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
B. Hình vuông là hình có trục đối xứng và có tâm đối xứng.
C. Hình thoi có một góc vuông là hình vuông.
D. Hình thang có hai cạnh bên bằng nhau là hình thang cân.
-
Câu 16:
Nếu tăng độ dài của một hình vuông lên lần thì diện tích hình vuông đó tăng lên mấy lần?
A. lần
B. lần
C. lần
D. lần
-
Câu 17:
Tính giá trị của biểu thức tại và .
A.
B.
C.
D.
-
Câu 18:
Phân tích đa thức sau thành nhân tử: .
A. .
B. .
C. .
D. .
-
Câu 19:
Tìm biết: .
A. hoặc .
B. hoặc .
C. hoặc .
D. hoặc .
-
Câu 20:
Rút gọn phân thức: .
A. .
B. .
C. .
D. .
-
Câu 21:
Thực hiện phép tính: .
A.
B.
C.
D.
-
Câu 22:
Hình vuông có độ dài đường chéo là . Độ dài cạnh hình vuông đó là:
A.
B.
C.
D.
-
Câu 23:
Một hình chữ nhật có diện tích . Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:
A.
B.
C.
D.
-
Câu 24:
Đa thức bằng:
A.
B.
C.
D.
-
Câu 25:
Kết quả của phép cộng: là:
A.
B.
C.
D.
-
Câu 26:
Kết quả rút gọn biểu thức: là:
A.
B.
C.
D.
-
Câu 27:
Số dư khi chia đa thức: cho đa thức là:
A.
B.
C.
D.
-
Câu 28:
Cho hình thang cân có thì bằng:
A.
B.
C.
D. Không tính được
-
Câu 29:
Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:
A. Hình thang cân
B. Hình chữ nhật
C. Hình thoi
D. Hình vuông
-
Câu 30:
Tính giá trị của biểu thức:
A.
B.
C.
D.
-
Câu 31:
Hình vuông có đường chéo bằng thì cạnh bằng:
A.
B.
C.
D.
-
Câu 32:
Hình thoi có hai đường chéo bằng và thì cạnh bằng:
A.
B.
C.
D.
-
Câu 33:
Phân thức: xác định với:
A.
B.
C.
D.
-
Câu 34:
Kết quả của phép tính: là:
A.
B.
C.
D.
-
Câu 35:
Phân tích đa thức thành nhân tử được kết quả là:
A.
B.
C.
D.
-
Câu 36:
Hình chữ nhật có . Khi đó, diện tích hình chữ nhật ABCD là:
A.
B.
C.
D.
-
Câu 37:
Số lượng trục đối xứng của hình vuông là:
A.
B.
C.
D.
-
Câu 38:
Tập hợp tất cả các giá trị của thỏa mãn: là:
A.
B.
C.
D.
-
Câu 39:
Một hình thoi có cạnh bằng và độ dài một đường chéo là . Khi đó, độ dài đường chéo còn lại của hình thoi là:
A.
B.
C.
D.
-
Câu 40:
Tứ giác là hình vuông khi tứ giác đó có:
A. Hai đường chéo bằng nhau và vuông góc với nhau
B. Bốn cạnh bằng nhau
C. Bốn cạnh bằng nhau và có một góc vuông
D. Bốn góc vuông












