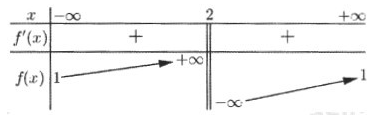
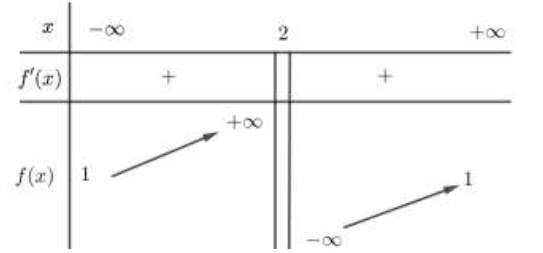
Cho hàm số \( f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\) (a,b,c thuộc R) có bảng biến thiên như sau:
Trong các số (a,b ) và (c ) có bao nhiêu số dương ?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào BBT ta thấy đồ thị hàm số có TCĐ:
\( x = 2 \Rightarrow - \frac{c}{b} = 2 \Leftrightarrow c = - 2b\)
TCN: \( y = 1 \Rightarrow \frac{a}{b} = 1 \Leftrightarrow a = b\)
Ta có: \( f\left( x \right) = \frac{{ax + 1}}{{bx + c}} \Rightarrow f'\left( x \right) = \frac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}}\)
Hàm số đồng biến trên các khoảng (−∞;2)(−∞;2) và (2;+∞)
\(\begin{array}{l} \Leftrightarrow y\prime > 0\forall x \ne 2\\ \Leftrightarrow \frac{{ac - b}}{{{{(bx + c)}^2}}} > 0\forall x \ne 2 \Leftrightarrow ac - b > 0 \Leftrightarrow b.( - 2b) - b > 0 \Leftrightarrow - 2{b^2} - b > 0\\ \Leftrightarrow 2{b^2} + b < 0 \Leftrightarrow - \frac{1}{2} < b < 0 \Rightarrow b < 0 \Rightarrow a < 0,c > 0 \end{array}\)
Vậy trong ba số a,b,c có 1 số dương.
Đáp án cần chọn là: C