Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số \(y=3 f(x+2)-x^{3}+3 x\) đồng biến trên khoảng nào dưới đây?
-
Câu 2:
Cho hàm số \(y=f(x)\) có đồ thị của hàm số \(y=f'(x)\)như hình vẽ bên
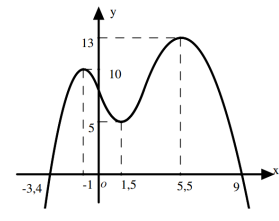
Hàm số \(y=39 f(x)-8 x^{3}+45 x^{2}-276 x+1\) đồng biến trên khoảng nào dưới đây?
-
Câu 3:
Cho hàm số y=f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên. Hàm số \(y=f \sqrt{x^{2}+2 x+3}-\sqrt{x^{2}+2 x+2}\) đồng biến trên khoảng nào dưới dây?
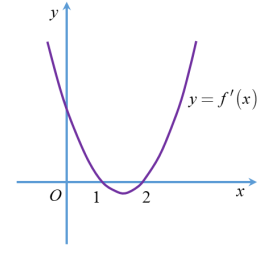
-
Câu 4:
Cho hàm số \(y=f(x), y=g(x)\) có đồ thị \(y=f^{\prime}(x), y=g^{\prime}(x)\) như hình vẽ dưới.
.png)
Hàm số \(y=f(x)-g(x)\)đồng biến trên khoảng nào dưới đây?
-
Câu 5:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}( x)=x^{2} (1-4 x^{2}), \quad \forall x \in \mathbb{R}\) . Hàm số y=f(cos x) đồng biến trên khoảng nào dưới đây?
-
Câu 6:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình \(\sqrt {\left( {1 + 2x} \right)\left( {3 - m} \right)} \; > \;m + 2{x^2} - 5x - 3\) nghiệm đúng với mọi \(x \in \left[ {\begin{array}{*{20}{c}}
{\frac{{ - 1}}{2};}3
\end{array}} \right]\)? -
Câu 7:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \({x^3} - 3{x^2} - 9x - m=0\) có đúng 1 nghiệm?
-
Câu 8:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y\; = \;\frac{{{x^2} - \left( {m + 1} \right) + 2m - 1}}{{x - m}}\) tăng trên từng khoảng xác định của nó?
-
Câu 9:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R?
\(y' = - \frac{1}{3}{x^3} - m{x^2} + \left( {2m - 3} \right)x - m + 2\)
-
Câu 10:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y\; = \;\frac{{x - m + 2}}{{x + 1}}\) giảm trên các khoảng mà nó xác định ?
-
Câu 11:
Cho hàm số \(y\; = \;\left| {x + 1} \right|\left( {x - 2} \right)\). Khẳng định nào sau đây là khẳng định sai?
-
Câu 12:
Cho hàm số \(y\; = \;x\; + \;{\cos ^2}\left( x \right)\). Khẳng định nào sau đây là khẳng định đúng?
-
Câu 13:
Cho hàm số \(y\; = \;\sqrt {3{x^2}\; - \;{x^3}} \). Khẳng định nào sau đây là khẳng định sai?
-
Câu 14:
Cho hàm số \(y\; = \;{x^3}\; + \;3{x^2}\; - \;9x\; + \;15\). Khẳng định nào sau đây là khẳng định sai?
-
Câu 15:
Hỏi hàm số \(y\; = \;\frac{3}{5}{x^5}\; - \;3{x^4}\; + \;4{x^3}\; - \;2\) đồng biến trên khoảng nào?
-
Câu 16:
Hỏi hàm số \(y\; = \;\frac{{{x^3}}}{3}\; - \;3{x^2}\; + \;5x\; - \;2\) nghịch biến trên khoảng nào?
-
Câu 17:
Hỏi hàm số \(y\; = \;\frac{{{x^2}\; - \;3x\; + \;5}}{{x\; + \;1}}\) nghịch biến trên các khoảng nào ?
-
Câu 18:
Hỏi hàm số nào sau đây luôn nghịch biến trên R?
-
Câu 19:
Cho hàm số \(y\; = \;\frac{{3x\; - \;1}}{{ - 4\; + \;2x}}\). Khẳng định nào sau đây là khẳng định đúng?
-
Câu 20:
Cho hàm số y = \({x^3}\; + \;3{x^2}\; - \;3x\; + \;2\). Khẳng định nào sau đây là khẳng định đúng?
-
Câu 21:
Cho hàm số \(y\; = \;\frac{{x + 1}}{{1 - x}}\) Khẳng định nào sao đây là khẳng đinh đúng?
-
Câu 22:
Cho hàm số \(y = {x^3} + 3{x^2} + mx + 1 - 2m.\).Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
-
Câu 23:
Tìm tất cả các giá trị của tham số m sao cho hàm số \(y\; = \;\frac{{\tan x\; + \;m}}{{\tan x\; + \;5}}\) nghịch biến trên \(\left( { - \frac{{\rm{\pi }}}{4};\frac{{\rm{\pi }}}{4}} \right)\)
-
Câu 24:
Cho hàm số \(y = \frac{{ - {x^3}}}{3} - \frac{{m{x^2}}}{2} - 2x + 1\)
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
-
Câu 25:
Cho hàm số \(y = {x^3}--{x^2} + \left( {m - 1} \right)x + m.\). Tìm điều kiện của tham số m để hàm số đồng biến trên R
-
Câu 26:
Hàm số \(y = x - \sqrt {{x^2} - 1} \) đồng biến trên khoảng nào?
-
Câu 27:
Tìm khoảng đồng biến của hàm số \(f\left( x \right) = x + {\cos ^2}x\)
-
Câu 28:
Cho hàm số \(y\; = \frac{{x + 1}}{{x - 1}}\;\left( 1 \right)\)
Khẳng định nào sau đây là khẳng định đúng?
-
Câu 29:
Khoảng nghịch biến của hàm số \(y = {x^4} - 2{x^2} - 1\) là:
-
Câu 30:
Tìm khoảng đồng biến của hàm số \(y = 2{x^3} - 9{x^2} + 12x + 3\)
-
Câu 31:
Hỏi hàm số \(y\; = \;\frac{{3x - 1}}{{x + 5}}\) đồng biến trên các khoảng nào?
-
Câu 32:
Cho đồ thị hàm số có dạng như hình vẽ.
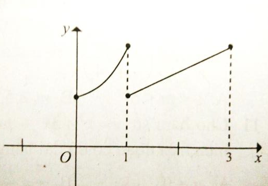
Hàm số đồng biến trên:
-
Câu 33:
Cho hàm số \(y = - {x^3} + 3{x^2} + 3mx - 1\), tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
-
Câu 34:
Tìm m để hàm số \(y\; = \;\frac{{ - mx + 2}}{{\;2x - m}}\) luôn nghịch biến trên khoảng xác định.
-
Câu 35:
Cho hàm số y = sin2x - 2x. Hàm số này
-
Câu 36:
Cho hàm số \(y = {x^4} - 2{x^2} + 3\). Kết luận nào sau đây đúng?
-
Câu 37:
Khoảng nghịch biến của hàm số \(y = \frac{{{x^3}}}{3} - 2{x^2} + 3x + 5\) là:
-
Câu 38:
Cho hàm số f(x) có đạo hàm \(f'\left( x \right)\; = \;\sqrt {x\left( {x - 1} \right){{\left( {x + 2} \right)}^2}} \)
Kết luận nào sau đây là đúng?
-
Câu 39:
Cho đồ thị hàm số \(y\; = \;\frac{{ - 2}}{x}\) như hình vẽ. Hàm số \(y\; = \;\frac{{ - 2}}{x}\) đồng biến trên
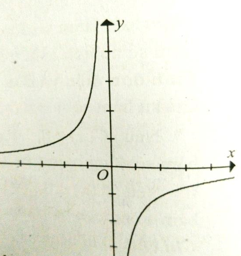
-
Câu 40:
Cho đồ thị hàm số y = −x3 như hình vẽ. Hàm số y = −x3 nghịch biến trên khoảng:
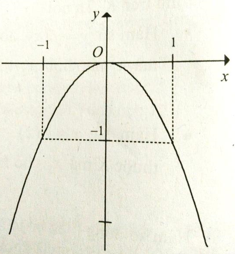
-
Câu 41:
Cho đồ thị hàm số với \(x\; \in \;\left[ { - \;\frac{\pi }{2}\;;\;\frac{{3\pi }}{2}} \right]\) như hình vẽ.
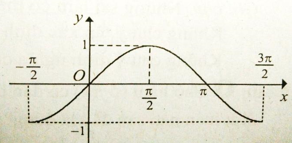
Tìm khoảng đồng biến của hàm số y = sinx với \(x\; \in \;\left[ { - \;\frac{\pi }{2}\;;\;\frac{{3\pi }}{2}} \right]\)
-
Câu 42:
Cho hàm số y =f(x) có bảng biến thiên như sau:
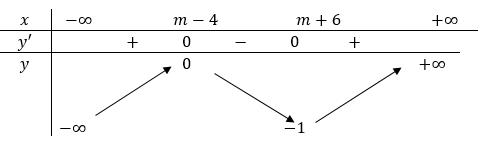
Có bao nhiêu số nguyên \(m \in(-40 ; 40)\) để hàm số \(\mathrm{y}=\mathrm{f}\left(\mathrm{x}^{2}\right)\) đồng biến trên khoảng \((2 ;+\infty)\)
-
Câu 43:
Cho hàm số \(f(x)=x^{3}-3 x+1 . \) . Có bao nhiêu số nguyên để hàm số \(y=f(m-x)+(m-1) x\) đồng biến trên khoảng (8;9)
-
Câu 44:
Cho hàm số y=f(x) . Hàm số \(y=f^{\prime}\left(3 x-\frac{1}{2}\right)\) nghịch biến trên khoảng có đồ thị như hình bên. Hàm số \(y=f(2 x-1)\) nghịch biến trên khoảng:
-
Câu 45:
Cho hàm số y =f(x) có bảng biến tiên như hình vẽ bên dưới đây. Hàm số\(y=[f(x)]^{2}-6 f(x)\) nghịch biến trên khoảng nào dưới đây
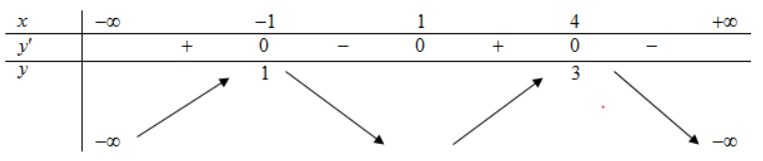
-
Câu 46:
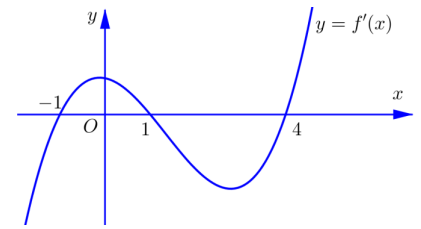
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ. Hàm số \(y=f\left(3-x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
-
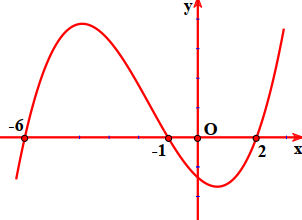
Câu 47:
Cho hàm số \(f(x)=x^{3}-m x^{2}-(m-6) x+1\) . Có bao nhiêu số nguyên dương m để hàm số\(y=f(x+\sqrt{x^{2}+1})\) đồng biến trên khoảng \((-\infty ;+\infty)\).
-
Câu 48:
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
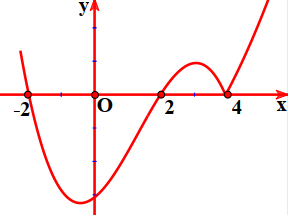
-
Câu 49:
Cho hàm số y=f(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
-
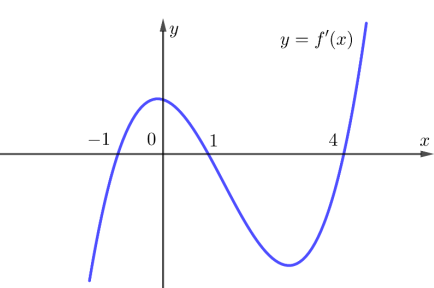
Câu 50:
Cho hàm số y=f(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Đặt \(h(x)=2 f(x)-x^{2}\) . Hàm số y=h(x) đồng biến trên khoảng nào dưới đây?