525 câu trắc nghiệm môn Toán rời rạc
tracnghiem.net chia sẻ 525 câu trắc nghiệm môn Toán rời rạc (có đáp án) dành cho các bạn sinh viên chuyên ngành có thêm tư liệu học tập, ôn tập chuẩn bị cho kì thi kết thúc học phần sắp diễn ra. Nội dung gồm những vấn đề cơ bản nhất của toán học rời rạc lý thuyết tổ hợp, lý thuyết đồ thị, lý thuyết độ phức tạp, đại số Boole.,…Để việc ôn tập trở nên hiệu quả hơn, các bạn có thể ôn theo từng phần trong bộ câu hỏi này bằng cách trả lời lần lượt các câu hỏi cũng như so sánh đáp và lời giải chi tiết được đưa ra. Sau đó các bạn hãy chọn tạo ra đề ngẫu nhiên để kiểm tra lại kiến thức mình đã ôn tập được nhé!
Chọn hình thức trắc nghiệm (30 câu/60 phút)
Chọn phần
-
Câu 1:
Thuật toán Dijkstra được dùng để:
A. Tìm đường đi ngắn nhất giữa các cặp đỉnh bất kì của đồ thị.
B. Tìm đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị
C. Tìm đường đi ngắn nhất giữa hai đỉnh của đồ thị.
D. Tìm đường đi ngắn nhất giữa một đỉnh nguồn và một đỉnh đích.
-
Câu 2:
Với đồ thị n đỉnh, độ phức tạp tính toán của thuật toán Dijkstra là:
A. O(n3 log2n)
B. O(n3)
C. O(n2)
D. O(n2 log2n)
-
Câu 3:
Thuật toán Floy được dùng để:
A. Tìm đường đi ngắn nhất giữa mọi cặp đỉnh của đồ thị.
B. Tìm đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị.
C. Tìm đường đi ngắn nhất giữa hai cặp đỉnh của đồ thị.
D. Tìm đường đi ngắn nhất giữa một đỉnh nguồn và một đỉnh đích
-
Câu 4:
Số cạnh của cây với 1000 đỉnh là:
A. 9900
B. 9999
C. 10000
D. 1001
-
Câu 5:
Để xây dựng cây khung nhỏ nhất của đồ thị, ta dùng:
A. Tìm kiếm theo chiều sâu (DFS).
B. Thuật toán Floyd.
C. Thuật toán Prim.
D. Thuật toán Dijsktra.
-
Câu 6:
Để xây dựng cây khung nhỏ nhất của đồ thị, ta dùng: (Chọn phương án đúng)
A. Thuật toán Dijsktra.
B. Tìm kiếm theo chiều rộng (BFS).
C. Tìm kiếm theo chiều sâu (DFS).
D. Thuật toán Prim.
-
Câu 7:
Thuật toán Kruskal áp dụng cho đồ thì G, n đỉnh sẽ dừng khi:
A. Kết nạp được n-1 cạnh vào cây khung.
B. Kết nạp được n cạnh vào cây khung.
C. Kết nạp được n – 2 cạnh vào cây khung.
D. Kết nạp được n - 3 cạnh vào cây khung.
-
Câu 8:
Sự giống nhau giữa thuật toán Prim và thuật toán Kruskal là:
A. Dừng khi kết nạp được tất cả các cạnh vào cây khung.
B. Dừng khi kết nạp được n đỉnh và n cạnh vào cây khung
C. Thuật toán chọn các cạnh có trọng số tối thiểu, liên thuộc với các đỉnh đã thuộc cây khung và không tạo ra chu trình.
D. Thuật toán xây dựng cây khung ngắn nhất.
-
Câu 9:
Sự khác nhau giữa thuật toán Prim và thuật toán Kruskal:
A. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc trong khi thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc.
B. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.
C. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình.
D. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, không liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.
-
Câu 10:
Hãy cho biết đồ thị nào dưới đây là một cây?
A.
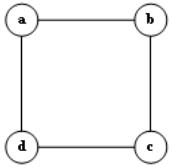
B.
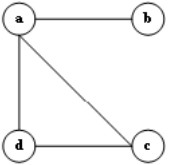
C.
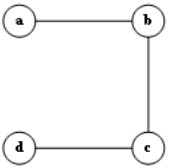
D.
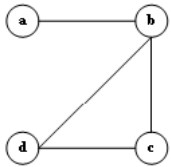
-
Câu 11:
Trong thuật toán Ford – Fullkerson giải bài toán luồng cực đại, bước tăng luồng thực hiện trên.
A. Các cạnh nằm ngoài đường đi đánh dấu.
B. Các cạnh nằm trên đường đi đánh dấu
C. Trên cạnh nối đỉnh phát với đỉnh thu.
D. Trên đỉnh phát và đỉnh thu.
-
Câu 12:
Trong thuật toán Ford – Fullkerson tìm luồng cực đại, thực hiện lặp đi lặp lại thao tác:
A. Đánh dấu các đỉnh và cải tiến luồng.
B. Nâng giá trị luồng.
C. Giảm giá trị luồng.
D. Giảm khả năng thông qua của các cạnh.
-
Câu 13:
Giá trị của luồng cực đại trong mạng:
A. Lớn hơn khả năng thông qua của mọi lát cắt.
B. Bằng khả năng thông qua của một lát cắt.
C. Không vượt quá khả năng thông qua của lát cắt hẹp nhất trong mạng.
D. Không vượt quá khả năng thông qua của lát cắt lớn nhất trong mạng.
-
Câu 14:
G là một đơn đồ thị phẳng liên thông n đỉnh, m cạnh, gọi r là số miền trong biểu diễn phẳng của G khi đó:
A. \(r ≠ m – n +2\)
B. \(r = m – n +2 \)
C. \(r ≥ m – n +2\)
D. \(r ≤ m – n +2\)
-
Câu 15:
Nếu một đơn đồ thị phẳng liên thông có n đỉnh, m cạnh \((n≥ 3)\) thì:
A. \(m ≠ 2n - 4\)
B. \(m = 2n - 4\)
C. \(m ≤ 2n - 4\)
D. \(m ≥ 2n - 4\)
-
Câu 16:
Theo định lý Ford – Fulkerson giá trị luồng cực đại từ điểm phát s đến điểm thu t.
A. Bằng khả năng thông qua của lát cắt hẹp nhất tách điểm s và t.
B. Bằng khả năng thông qua của lát cắt lớn nhất tách điểm s và t.
C. Không vượt quá khả năng thông qua của lát cắt lớn nhất tách điểm s và t.
D. Tất cả các đáp án đều sai
-
Câu 17:
Đồ thị G = (V,E) được gọi là đơn đồ thị nếu.
A. giữa hai đỉnh bất kỳ \(i,j \in V\), có nhiều nhất một cạnh, có kể đến thứ tự các đỉnh.
B. Giữa hai đỉnh bất kỳ \(i,j \in V\), có nhiều nhất một cạnh.
C. Giữa hai đỉnh bất kỳ \(i,j \in V\), có thể có nhiều hơn một cạnh, có kể đến thứ tự các đỉnh.
D. Giữa hai đỉnh bất kỳ \(i,j \in V\), có thể có nhiều hơn một cạnh, không kể đến thứ tự các đỉnh.
-
Câu 18:
Nếu G = (V,E) là một đơn đồ thị vô hướng thì:
A. G không có khuyên, không có cạnh bội.
B. G không có khuyên, có thể có cạnh bội.
C. G có khuyên, không có cạnh bội.
D. G có khuyên, có thể có cạnh bội.
-
Câu 19:
Đồ thị G = (V,E) được gọi là đồ thị vô hướng nếu:
A. Tồn tại một cạnh của G là cạnh vô hướng
B. Mọi cạnh của G là cạnh vô hướng
C. Có hai cạnh của G là cạnh vô hướng
D. Mọi cạnh của G là cạnh có hướng
-
Câu 20:
Nếu G = (V,E) là một đơn đồ thị vô hướng thì: (Chọn phương án đúng)
A. Ma trận kề gồm các phần tử đối xứng nhau qua đường chéo chính
B. Ma trận kề gồm các phần tử không đối xứng nhau qua đường chéo chính
C. Các phần tử trên đướng chéo chính bằng 1
D. Các phần tử trên đường chéo phụ bằng 1
-
Câu 21:
Nếu G = (V,E) là một đa đồ thị vô hướng thì:
A. G không có khuyên
B. G chứa cạnh bội
C. G không có cạnh bội.
D. G có thể có cạnh có hướng
-
Câu 22:
Ta gọi đỉnh v là đỉnh treo trong đồ thị vô hướng G = (V,E) A).
A. Nếu bậc của đỉnh v là 0.
B. Nếu bậc của đỉnh v là một số lẻ.
C. Nếu bậc của đỉnh v là một số chẵn.
D. Nếu bậc của đỉnh v là 1.
-
Câu 23:
Đồ thị vô hướng G = (V,E) được gọi là liên thông nếu.
A. Giữa hai đỉnh bất kỳ \(u,v \in V\) luôn tồn tại đường đi từ u đến v.
B. Nếu \(u,v \in V\), thì tồn tại v khác u sao cho v liên thông với u.
C. Nếu \(u,v \in V\), thì với mọi v khác u đều kề với u.
D. Nếu \(u,v \in V\), thì tồn tại đỉnh v khác u kề với u.
-
Câu 24:
Đồ thị có hướng G =(V,E) được gọi là liên thông mạnh nếu:
A. Giữa hai đỉnh bất kỳ \(u,v \in V\) luôn tìm được đường đi từ u đến v và đường đi từ v đến u.
B. Giữa hai đỉnh bất kỳ \(u,v \in V\) luôn tìm được đường đi từ u đến v
C. Giữa hai đỉnh bất kỳ \(u,v \in V\) luôn tìm được đường đi từ v đến u
D. Giữa hai đỉnh bất kỳ \(u,v \in V\) không tồn tại đường đi từ u đến v
-
Câu 25:
Ta nói cặp hai đỉnh (u,v) là cạnh vô hướng của đồ thị G = (V,E) nếu:
A. \(u, v \times V\) và u, v có thứ tự
B. \(u, v \times V\) và u, v có thứ tự
C. \(u, v \times V\) và u, v không có thứ tự
D. \(u, v \times V\) và u, v không có thứ tự
-
Câu 26:
Ma trận kề của đồ thị vô hướng G = (V,E) có tính chất:
A. Là ma trận đơn vị.
B. Là ma trận đối xứng.
C. Là ma trận không đối xứng.
D. Là ma trận đường chéo trên.
-
Câu 27:
Ma trận kề của đồ thị có hướng không phải là:
A. Ma trận đối xứng.
B. Ma trận đướng chéo trên.
C. Ma trận không đối xứng.
D. Ma trận đường chéo dưới.
-
Câu 28:
Trong biểu diễn đồ thị bởi danh sách kề, mỗi đỉnh của đồ thị có một danh sách:
A. Các cạnh kề với đỉnh đó
B. Các bậc của đỉnh kề với đỉnh đó
C. Các đỉnh kề với đỉnh đó
D. Các cạnh kề với cạnh đó
-
Câu 29:
Ma trận kề của một đơn đồ thị vô hướng đầy đủ là:
A. Ma trận tam giác trên.
B. Ma trận tam giác dưới
C. Ma trận có các phần tử trên đường chéo chính bằng 0, các phần tử khác bằng 1.
D. Ma trận có các phần tử trên đường chéo chính bằng 1, các phần tử khác bằng 0.
-
Câu 30:
Cho ma trận kề A[n,n] biểu diễn đồ thị G vô hướng, n đỉnh, giá trị A[i,j] của ma trận kề xác định:
A. Có cạnh giữa đinh i và đỉnh j
B. Có cạnh giữa đinh j và đỉnh i
C. Không có cạnh giữa đinh i và đỉnh j
D. Không có cạnh giữa đinh i và đỉnh j














