525 câu trắc nghiệm môn Toán rời rạc

A. Không có chu trình. 

B. Không có đỉnh cô lập

C. Không có cạnh cầu

D. Không có đỉnh treo

A. trong đó có một đỉnh cô lập. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung e.

B. trong đó có duy nhất một đỉnh s không có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t không có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung 

C. trong đó có duy nhất một đỉnh s có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung

D. trong đó có duy nhất một đỉnh s có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t không có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung 

A. Tất cả các đỉnh của G.

B. Tất cả các đỉnh của G trừ đỉnh phát s.

C. Tất cả các đỉnh của G rừ đỉnh thu t.

D. Tất cả các đỉnh của G trừ đỉnh phát s và đỉnh thu t.

A. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x Y và vj x X, vi x Y

B. Tập hợp tất cả các cung (vi, vj) sao cho hoặc vi x X, vj x Y hoặc vj x X, vi x Y

C. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x X hoặc vj x X, vi x Y

D. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x Y hoặc vj x Y, vi x Y

A. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi ra khỏi đỉnh s

B. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi vào đỉnh t

C. khả năng thông qua của lát cắt (X,Y) lớn nhất. 

D. khả năng thông qua của lát cắt (X,Y) bé nhất.

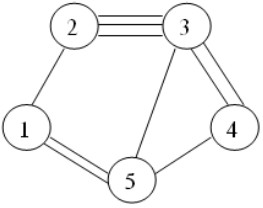
A. 3, 3, 4, 6, 4

B. 3, 4, 6, 4, 4

C. 3, 4, 6, 4, 5

D. 3, 4, 5, 4, 4

A. 60

B. 45

C. 30

D. 20

A. 2, 4, 3, 1, 4, 2, 5

B. 3, 4, 2, 1, 4, 2, 6

C. 5, 2, 2, 1, 3, 2, 4

D. 2, 1, 4, 3, 4, 2, 7

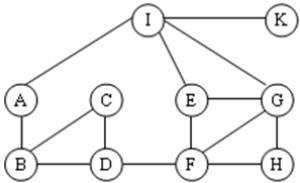
A. I, A, E, G, K, B, C, F, H, D

B.  I, A, E, G, C, K, B, F, H, D 

C. I, A, B, C, D, E, G, H, F, K

D.  I, A, B, D, E, G, C, F, H, K

A. K, A, B, C, D, E, F, G, H, I

B. K, A, C, E, G, B, D, F, H, I

C. K, I, E, G, F, H, A, B, C, D

D. K, I, A, E, G, B, C, F, H, D

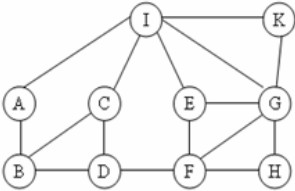
A. I, A, C, H, E, G, B, D, F, K

B. I, A, B, C, D, E, G, F, H, K

C. I, A, C, K, E, G, B, D, F, H

D. I, E, F, G, H, A, B, C, D, K

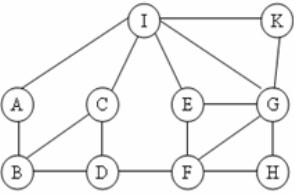
A. H, G, F, D, E, F, A, B, C, I

B. H, F, G, E, K, I, A, C, B, D

C. H, G, F, B, D, E, K, A, C, I

D. H, E, F, G, H, I, A, B, C, D

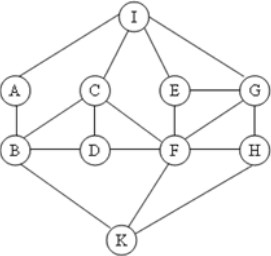
A. I, A, D, E, G, B, C, F, H, K

B. I, A, B, C, D, E, F, G, H,K 

C. I, E, F, G, H, A, B, C, D, K

D. I, A, C, E, G, B, D, F, H, K

A. K, B, D, F, H, A, C, E, G, I

B. K, B, A, C, D, F, E, G, H, I

C. K, B, F, H, A, C, D, E, G, I

D. K, E, F, G, H, A, B, C, D, I

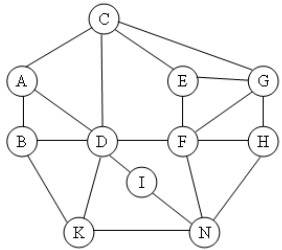
A. C, A, B, E, F, D, G, H, K, C, N

B. C, A, B, K, N, I, D, E, F, H, G

C. C, A, E, G, B, D, F, H, K, I, N 

D. C, A, E, G, F, H, N, B, D, I, K 

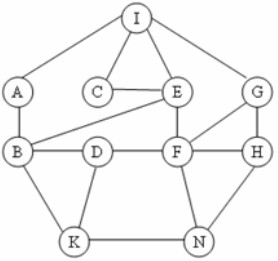
A. I, A, C, E, G, B, F, H, D, K, N

B.  I, C, E, F, G, K, H, N, B, D, A

C. I, G, B, F, N, K, E, C, D, H, A

D. I, G, H, N, K, B, A, C, E, F, D

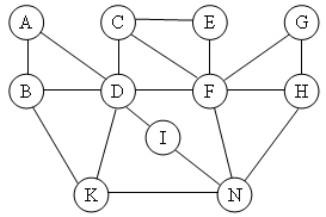
A. A, B, K, D, C, E, F, G, H, N, I

B. A, B, D, K, I, N, C, E, G, H, F

C. A, C, E, F, D, B, I, N, K, H, B

D. A, K, N, D, F, H, G, E, C, I, B

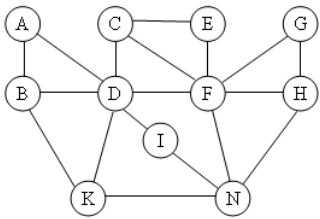
A. G, H, I, N, K, B, A, C, D, E, F

B. G, H, N, K, B, A, D, C, E, F, I

C. G, H, N, K, B, A, C, D, E, I, F

D. G, A, B, C, D, E, F, N, K, H, I 

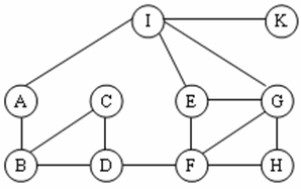
A. K, I, A, C, E, G, B, D, F, H 

B. K, I, A, B, C, D, E, F, G, H

C. K, I, A, B, C, D, F, H, G, E

D. K, A, C, D, B, I, G, H, F, E

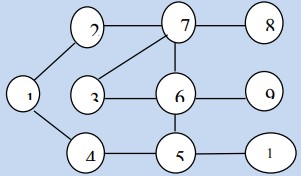
A. 1, 2, 4, 7, 3, 6, 8, 5, 9, 10

B. 1, 7, 6, 3, 9, 8, 5, 10, 4, 2

C. 1, 2, 6, 4, 5, 10, 9, 8, 3, 7

D. 1, 2, 4, 7, 8, 9, 5, 10, 3, 6

A. 2, 1, 3, 4, 5, 10, 6, 9, 7, 8

B. 2, 1, 7, 4, 3, 6, 8, 5, 9, 10

C. 2, 1, 3, 5, 4, 10, 6, 9, 7, 8

D. 2, 1, 7, 3, 6, 9, 4, 5, 8, 10 

A. 1, 2, 7, 4, 5, 10, 3, 6, 9, 8

B. 1, 2, 3, 6, 9, 4, 5, 10, 8, 7

C. 1, 2, 3, 4, 5, 10, 6, 9, 7, 8

D. 1, 2, 7, 8, 3, 6, 9, 5, 10, 4 

A. 10, 5, 4, 1, 2, 3, 6, 9, 8, 7

B. 10, 5, 4, 1, 2, 7, 8, 6, 9, 3

C. 10, 4, 5, 2, 1, 6, 9, 7, 8, 3

D. 10, 4, 5, 1, 2, 3, 6, 9, 8, 7

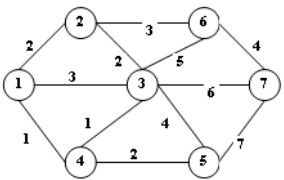
A. T = { (1,2), (1, 4), (2, 3), (2, 6), (6,3), (6, 7) } B)

B. T = { (1,2), (1, 4), (1, 3), (2, 6), (4,5), (6, 7) }

C. T = { (1,2), (1, 4), (2, 4), (2, 6), (4,5), (6, 7) }

D. T = { (1,2), (1, 4), (2, 3), (4,5) ,(2, 6), (6, 7) }

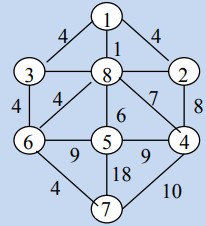
A. T = {(3,6),(1,8),(8,2), (3,6), (6,7), (8,5), (5,7)}

B. T = {(1,2),(3,8),(8,5), (3,6), (6,7), (2,4), (4,7)}

C. T = {(5,7),(5,6),(8,2), (3,6), (6,7), (8,5), (8,4)}

D. T = {(1,8),(3,8),(8,2), (3,6), (6,7), (8,5), (8,4)}

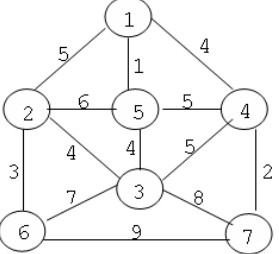
A. T ={(2,5)(2,6)(2,3)(6,2)(4,1)(5,4)}

B. T ={(5,3)(3,7)(2,3)(6,2)(4,1)(7,4)}

C. T ={(5,1)(3,5)(2,3)(6,2)(4,1)(7,4)}

D. T ={(4,7)(3,5)(2,3)(6,2)(4,1)(3,6)}

A. Nó là hội của các biểu thức hội cơ bản

B. Nó là hội của các biểu thức tuyển cơ bản

C. Nó là tuyển của các biểu thức hội cơ bản

D. Nó là tuyển của các biểu thức tuyển cơ bản

A. Nó là hội của các biểu thức hội cơ bản

B. Nó là hội của các biểu thức tuyển cơ bản

C. Nó là tuyển của các biểu thức hội cơ bản

D. Nó là tuyển của các biểu thức tuyển cơ bản

A. \(F = {q_1} \vee {q_2} \vee ... \vee {q_n}\) với  qj = pj hoặc \({q_j} = \overline {{p_j}} (j = 1,...,n)\)

B. \(F = {q_1} \vee {q_2} \vee ... \vee {q_n}\)

C. \(F = {q_1} \wedge {q_2} \wedge ... \wedge {q_n}\)

A. \((P \wedge Q) \vee (P \vee Q)\)

B. \((P \wedge Q) \vee (\overline {P \vee Q} )\)

C. \((\overline {P \wedge Q} ) \vee (P \vee Q)\)

D. \((\overline {P \wedge Q} ) \wedge (P \vee Q)\)