525 câu trắc nghiệm môn Toán rời rạc
tracnghiem.net chia sẻ 525 câu trắc nghiệm môn Toán rời rạc (có đáp án) dành cho các bạn sinh viên chuyên ngành có thêm tư liệu học tập, ôn tập chuẩn bị cho kì thi kết thúc học phần sắp diễn ra. Nội dung gồm những vấn đề cơ bản nhất của toán học rời rạc lý thuyết tổ hợp, lý thuyết đồ thị, lý thuyết độ phức tạp, đại số Boole.,…Để việc ôn tập trở nên hiệu quả hơn, các bạn có thể ôn theo từng phần trong bộ câu hỏi này bằng cách trả lời lần lượt các câu hỏi cũng như so sánh đáp và lời giải chi tiết được đưa ra. Sau đó các bạn hãy chọn tạo ra đề ngẫu nhiên để kiểm tra lại kiến thức mình đã ôn tập được nhé!
Chọn hình thức trắc nghiệm (30 câu/60 phút)
Chọn phần
-
Câu 1:
Cho một tập S = {0, 1, 2}, câu nào dưới đây là đúng:
A. Có 2 cách phân hoạch tập S
B. Có 3 cách phân hoạch tập S.
C. Có 4 cách phân hoạch tập S.
D. Có 5 cách phân hoạch tập S.
-
Câu 2:
Cho tập A= {a, b, c, d}, hỏi quan hệ nào trong số các quan hệ trên A dưới đây có tính phản đối xứng?
A. R = {(a,a), (a,b), (b,c), (b,d), (c,c), (c,b), (d,a), (d,b)}
B. R = {(a,a), (a,c), (a,d), (c, b),(c,c), (d,b), (d,c)}
C. R = {(a,a), (a,b), (a,c), (b,b), (b,c), (c,c), (c,a), (d,d), (d,b)}
D. R = {(a,a), (a,c), (b,b), (b,d), (c,c), (c,a), (d,d), (d,c)}
-
Câu 3:
Cho quan hệ R = {(a,b)| a ≡ b(mod 5)} trên tập {-12, -11, …,11, 12}. Hãy xác định [2]R?
A. {-9, -3, 2, 7, 12}
B. {-12, -7, -2, 2, 7, 12}
C. {-8, -3, 2, 7, 12}
D. {2}
-
Câu 4:
Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A được xác định như sau: Với mọi a, b A, aRb khi và chỉ khi hiệu a - b là một số chẵn. Quan hệ R là:
A. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6), (1, 3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}
B. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6), (3,1),(5, 1), (4, 2), (6,2), (5,3), (6,4)}
C. R= {(1, 3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}
D. R= {( (3,1), (5, 1), (4, 2), (6,2), (5,3), (6,4)}
-
Câu 5:
Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A với:
R= {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (1,3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}
Ma trận biểu diễn R là:
A. \(\left[ {\begin{array}{*{20}{c}} 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1 \end{array}} \right]\)
B. \(\left[ {\begin{array}{*{20}{c}} 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&1&1&0&1 \end{array}} \right]\)
C. \(\left[ {\begin{array}{*{20}{c}} 1&0&1&1&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1 \end{array}} \right]\)
D. \(\left[ {\begin{array}{*{20}{c}} 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0\\ 0&1&0&1&0&1\\ 1&0&1&0&1&0 \end{array}} \right]\)
-
Câu 6:
Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A với:
R= {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (1,3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}
Đồ thị biểu diễn quan hệ R là
A.
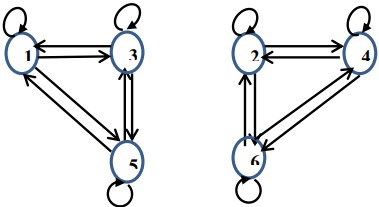
B.
C.
-
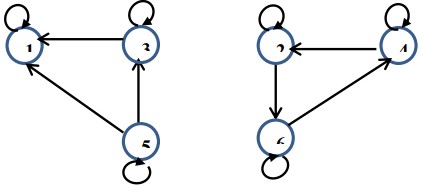
Câu 7:
Nhận xét nào sau đây là SAI:
A. Một quan hệ có tính phản xạ khi và chỉ khi ma trận biểu diễn nó có tất cả các phần tử trên đường chéo chính đều bằng 1
B. Một quan hệ có tính đối xứng khi và chỉ khi ma trận biểu diễn nó là một ma trận đối xứng qua đường chéo chính
C. Một quan hệ có tính phản xạ khi và chỉ khi đồ thị biểu diễn nó tại mỗi đỉnh đều có khuyên
D. Một quan hệ có tính bắc cầu khi và chỉ khi đồ thị biểu diễn nó có cung đi từ đỉnh a đến đỉnh b thì cũng có cung đi từ đỉnh b đến đỉnh c
-
Câu 8:
Cho A là một tập hữu hạn khác rỗng. Quan hệ R⊆ AxA. Phát biểu nào sau đây là ĐÚNG:
A. Quan hệ R có tính phản xạ nếu mọi phần tử a thuộc A đều có quan hệ R với chính nó.
B. Quan hệ R có tính đối xứng nếu mọi a, b thuộc A thì a phải có quan hệ R với b.
C. Quan hệ R có tính bắc cầu nếu mọi a, b, c thuộc A thì a phải có quan hệ R với b và b phải có quan hệ R với c
-
Câu 9:
Cho biết quan hệ nào là quan hệ tương đương trên tập {a, b, c, d}:
A. {(a, a), (b, b), (c, c), (d, d), (a, b), (a, c), (a, d)}
B. {(a, a), (b, b), (c, c), (d, d), (a, b), (b, a)}
C. {(a, a), (a, c), (c, a), (c, c), (c, d), (d, c), (d, d)}
D. {(a, a), (b, b), (c, c), (d, d) , (c, d), (d, c), (d, a), (b, d)}
-
Câu 10:
Cho A ={11, 12, 13, 14, 15}. Quan hệ R được xác định: \(\forall a,b \in A,aRb \Leftrightarrow a + b = 2k(k = 1,2,...)\). Quan hệ R được biểu diễn là:
A. {(11, 11), (12, 12), (13, 13), (14, 14), (11, 13), (13, 11), (11, 15), (15, 11), (12, 14), (14, 12)}
B. {(11, 11), (12, 12), (13, 13), (14, 14), (15, 15), (11, 13), (11, 15), (13, 15), (12, 14)}
C. {(11, 13), (13, 11), (11, 15), (15, 11), (13, 15), (15, 13), (12, 14), (14, 12)}
D. {(11,11), (12, 12), (13, 13), (14, 14), (15, 15), (11,13), (13, 11), (11, 15), (15, 11), (13, 15), (15, 13), (12, 14), (14, 12)}
-
Câu 11:
Cho A = {11, 12, 13, 14, 15}. Trên A xác định quan hệ R như sau: \(\forall a,b \in A,aRb \Leftrightarrow a + b = 2k + 1(k = 1,2,...)\). Quan hệ R được biểu diễn là:
A. {(11, 12), (11, 14), (12, 13), (12, 15)}
B. {(11, 11), (12, 12), (13, 13), (14,14), (15,15), (11, 12), (11, 14), (12, 13), (12, 15)}
C. {(11, 12), (12, 11), (11, 14), (14, 11), (12, 15), (15, 12)}
D. {(11, 12), (12, 11), (11, 14), (14, 11), (12, 15), (15, 12), (13, 14), (14, 13), (12, 13), (13, 12), (14, 15), (15, 14)}
-
Câu 12:
Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A1 = {1}, A2 = {2}, A3 = {3, 4}, A4 = {5, 6}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3, A4 là:
A. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (3, 4), (4, 3), (5, 6), (6, 5)}
B. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (1, 2), (2, 1), (3, 4), (4, 3)}
C. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (2, 3), (3, 2), (4, 5), (5, 4)}
D. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (4, 5), (5, 4), (1, 2), (2, 1), (1, 3), (3, 1)}
-
Câu 13:
Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A1 = {1, 2, 3}, A2 = {4, 5}, A3 = {6}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3 là:
A. {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (1,3), (3,1), (2,3), (3,2), (4,5), (5,4)}
B. {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (1,3),(3, 1),(5, 6), (6,5)}
C. {(1,1), (1,2), (2,2), (3,4), (3,3), (5,6), (4,4), (5,5), (6,6)}
D. {(1,1), (2,2), (3,3), (4,4), (5,5), (6, 6), (1,2), (2,1), (1,3), (3,1), (3,4), (4,3)}
-
Câu 14:
Cho tập A = {1, 2, 3, 4, 5, 6} và quan hệ tương đương R trên A như sau: R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (4,5), (5,4)}. Xác định phân hoạch do R sinh ra:
A. A1 = {1, 2, 3}, A2 = {4, 5, 6}
B. A1 = {1, 2}, A2 = {3}, A3 = {4,5}, A4 = {6}
C. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5, 6}
D. A1 = {1,2}, A2 = {3, 4}, A3 = {5, 6}
-
Câu 15:
Cho A = {1, 2, 3, 4, 5, 6}. Quan hệ R được xác định: \(\forall a,b \in A,aRb \Leftrightarrow a + b = 2k(k = 1,2,...)\). Xác định phân hoạch do R sinh ra:
A. A1 = {1,3}, A2 = {2,4}, A3 = {5}
B. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}
C. A1 = {1}, A2 = {2}, A3 = {3}, A4 = {4},A5 = {5}
D. A1 = {1,3,5}, A2 = {2,4}
-
Câu 16:
Cho tập A ={1,2,3,4,5}, hãy tìm ma trận biểu diễn quan hệ R trên A sau đây: R = {(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(3,1),(3,2),(2,3)}
A. \(\left[ {\begin{array}{*{20}{c}} 1&0&1&0&0\\ 0&1&1&0&0\\ 1&1&1&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{array}} \right]\)
B. \(\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&1&0&0\\ 0&1&1&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{array}} \right]\)
C. \(\left[ {\begin{array}{*{20}{c}} 1&1&0&0&0\\ 1&1&0&0&0\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{array}} \right]\)
D. \(\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&1&0&0\\ 0&1&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{array}} \right]\)
-
Câu 17:
Hãy liệt kê quan hệ R trên tập hợp {1,2,3,4,5} biết ma trận biểu diễn như sau:
\(\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&1&0&0\\ 0&1&1&0&1\\ 0&0&0&1&1\\ 0&0&1&1&1 \end{array}} \right]\)
A. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(2,4),(4,2),(4,5),(5,4)}
B. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4)}
C. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(3,5),(5,3),(4,5),(5,4)}
D. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,4),(4,2),(3,4),(4,3),(4,5),(5,4)}
-
Câu 18:
Cho quan hệ R = {(a,b) | a b (mod n) } trên tập số nguyên dương. Hỏi R KHÔNG có tính chất nào?
A. Phản xạ
B. Đối xứng
C. Bắc cầu
D. Phản đối xứng
-
Câu 19:
Cho tập A = {1, 2, 3, 4, 5}.Trong các quan hệ trên tập A cho dưới đây, quan hệ nào là quan hệ tương đương?
A. {(1,1), (1,2), (1,3), (2,2), (2,1), (2,3), (3,3), (1,5), (5,1)}
B. {(1,1), (2,2), (3,3), (4,4), (5,5), (1,2), (2,1), (1,3), (3,1)}
C. {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)}
D. {(1,1), (2,2), (3,3), (4,4), (5,5), (2,1), (1,2), (3,4), (4,3)}
-
Câu 20:
Cho quan hệ R = {(a,b)| a ≡ b(mod 4)} trên tập {-10, -9, …,9, 10}. Hãy xác định [2]R?
A. {-10, -6, -2, 2, 6, 10}
B. {2, 4, 6, 8, 10}
C. {-10, -8, -6, -4,-2}
D. {-8, -6, -4, -2, 2, 4, 6, 8}
-
Câu 21:
Cho tập S và một phân hoạch của S gồm 3 tập A1, A2, A3. Câu nào dưới đây là sai:
A. \({A_1} \cap {A_2} = \emptyset \)
B. \({A_1} \cup {A_2} = S \)
C. \({A_2} - {A_3} = {A_2}\)
D. \({A_1} \cup {A_2} \cup {A_3} = S\)
-
Câu 22:
Cho tập A = {-12, -11, …, 11, 12}, và quan hệ R = {(a,b)| a ≡ b (mod 4)}. Hãy cho biết tập nào trong số các tập sau là lớp tương đương của phần tử -7?
A. {-9, -5, -1, 3, 7, 10}
B. {-11, -7, -3, 1, 5, 9}
C. {-11, -3, 1, , 3, 9}
D. {-9, 6, 1, -8, 3, -5, 0, -12}
-
Câu 23:
Cho một tập S = {1, 2, 3, 4}, câu nào dưới đây là đúng:
A. Có 10 cách phân hoạch tập S.
B. Có 11 cách phân hoạch tập S.
C. Có 12 cách phân hoạch tập S
D. Có 13 cách phân hoạch tập S
-
Câu 24:
Cho tập A= {5, 6, 7, 8}, hỏi quan hệ nào trong số các quan hệ trên A dưới đây có tính phản đối xứng?
A. R = {(5,5), (5,7), (5,8), (7,6), (7,7), (8,6), (8,7)}
B. R = {(5,5), (5,6), (6,7), (7,6) ,(6,8), (7,7), (8,5), (8,6)}
C. R = {(5,5), (5,6), (5,7), (7,5),(6,6), (6,7), (7,7), (8,8), (8,6)}
D. R = {(5,5), (5,7), (7,5), (6,6), (6,8), (7,7), (8,8), (8,7)}
-
Câu 25:
Cho quan hệ R = {(a,b)| a ≡ b(mod 6)} trên tập {-15, -11, …,11, 15}. Hãy xác định [5]R?
A. {-13, -7, -1, 5, 11}
B. {-10, -4, 2, 5, 8, 14}
C. {-15, -9, -3, 3, 5, 9, 15}
D. {-14, -8, -2, 4, 5, 10}
-
Câu 26:
Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A được xác định như sau: Với mọi a, b \(\in\) A, aRb khi và chỉ khi hiệu 2a-b = 0. Quan hệ R là:
A. R= {(1, 2), (2, 4), (3, 6)}
B. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6)}
C. R= {(1, 2), (2,1),(2, 4), (4, 2), (3, 6), (6, 3)}
D. R= {(1,1), (2, 2), (3,3), (4,4), (5,5), (6,6), (2,4), (4,6)}
-
Câu 27:
Giả sử P và Q là 2 mệnh đề. Tuyển của 2 mệnh đề (P v Q) là một mệnh đề… ?
A. Chỉ đúng khi cả P và Q cùng đúng
B. Chỉ sai khi cả P và Q cùng sai
C. Chỉ đúng khi P đúng Q sai
D. Chỉ sai khi P đúng Q sai
-
Câu 28:
Hãy cho biết khẳng định nào sau đây không phải là 1 mệnh đề?
A. 2 + 3 < 4
B. 3 là 1 số chẵn
C. Cho x là một số nguyên dương
D. 1 - 2 < 0
-
Câu 29:
Giả sử P và Q là 2 mệnh đề. Hội của 2 mệnh đề (P ^ Q) là một mệnh đề…?
A. Nhận chân trị đúng khi cả P và Q cùng đúng. Chỉ sai khi 1 trong 2 mệnh đề P, Q nhận chân trị sai
B. Nhận chân trị đúng khi ít nhất 1 trong 2 mệnh đề P và Q đúng. Chỉ sai cả 2 mệnh đề P, Q nhận chân trị sai.
C. Chỉ nhận chân trị đúng khi P đúng Q sai hoặc Q đúng P sai.
D. Nhận chân trị sai khi 1 trong 2 mệnh đề hoặc cả 2 mệnh đề P và Q sai. Chỉ đúng khi và chỉ khi cả 2 mệnh đề P, Q nhận chân trị đúng.
-
Câu 30:
Giả sử P và Q là 2 mệnh đề, P→Q là một mệnh đề…?
A. Chỉ nhận chân trị sai khi P đúng Q sai. Nhận chân trị đúng trong các trường hợp còn lại.
B. Chỉ nhận chân trị sai khi P sai Q đúng. Nhận chân trị đúng trong các trường hợp còn lại.
C. Chỉ nhận chân trị đúng khi P sai Q đúng. Nhận chân trị sai trong các trường hợp còn lại.
D. Nhận chân trị đúng khi 1 trong 2 mệnh đề nhận chân trị đúng, sai trong các trường hợp còn lại.
Đề thi liên quan
500 câu trắc nghiệm Phương pháp nghiên cứu khoa học
Bộ 500 câu trắc nghiệm ôn thi Phương pháp nghiên cứu khoa học có đáp án sẽ giúp cho các bạn sinh viên có thêm tư liệu ôn tập và thi cử đạt kết quả cao.
60+ câu trắc nghiệm Giáo dục học đại cương
Sưu tầm và chia sẻ 68 câu hỏi trắc nghiệm Giáo dục học đại cương có đáp án, nhằm giúp các bạn sinh viên chuyên ngành chuẩn bị cho kì thi sắp tới.
1500 câu trắc nghiệm Kinh tế Vĩ mô
Hệ thống các câu hỏi trắc nghiệm ôn thi môn Kinh tế Vĩ mô dành cho sinh viên đại học, cao đẳng thuộc khối ngành kinh tế, và đặc biệt còn là trợ thủ đắc lực cho học viên ôn thi cao học.
