525 câu trắc nghiệm môn Toán rời rạc
tracnghiem.net chia sẻ 525 câu trắc nghiệm môn Toán rời rạc (có đáp án) dành cho các bạn sinh viên chuyên ngành có thêm tư liệu học tập, ôn tập chuẩn bị cho kì thi kết thúc học phần sắp diễn ra. Nội dung gồm những vấn đề cơ bản nhất của toán học rời rạc lý thuyết tổ hợp, lý thuyết đồ thị, lý thuyết độ phức tạp, đại số Boole.,…Để việc ôn tập trở nên hiệu quả hơn, các bạn có thể ôn theo từng phần trong bộ câu hỏi này bằng cách trả lời lần lượt các câu hỏi cũng như so sánh đáp và lời giải chi tiết được đưa ra. Sau đó các bạn hãy chọn tạo ra đề ngẫu nhiên để kiểm tra lại kiến thức mình đã ôn tập được nhé!
Chọn hình thức trắc nghiệm (30 câu/60 phút)
Chọn phần
-
Câu 1:
Xác định chân trị của biểu thức (\(\neg \)X→\(\neg \)Y) \( \wedge \) (\(\neg \)Y → \(\neg \)Z) và (\(\neg \)X → \(\neg \)Z) khi X = Y=0, Z= 1?
A. 1 và 1
B. 0 và 0
C. 1 và 0
D. 0 và 1
-
Câu 2:
Xác định chân trị của biểu thức (\(\neg \)X→Y ) \(\wedge \) (\(\neg \)Y → Z ) và (\(\neg \)X →Z) khi X = Y=0, Z= 1?
A. 1 và 1
B. 0 và 0
C. 1 và 0
D. 0 và 1
-
Câu 3:
Câu nào sau đây KHÔNG là một mệnh đề:
A. Hôm nay không phải Thứ hai
B. Lan học giỏi Tin học
C. Không phải Hiếu được khen thưởng
D. Thật vui vì Lan ở nhà.
-
Câu 4:
Câu nào sau đây KHÔNG phải là một mệnh đề:
A. Có ai ở nhà không?
B. Hà Nội là thủ đô của Việt Nam
C. Hôm nay trời mưa
D. 2+1=5
-
Câu 5:
Câu nào dưới đây KHÔNG là một mệnh đề:
A. An là sinh viên khoa CNTT
B. An không phải học Trí tuệ nhân tạo
C. X là sinh viên không phải học Trí tuệ nhân tạo
D. An là sinh viên CNTT nhưng không phải học Trí tuệ nhân tạo.
-
Câu 6:
Câu nào sau đây là một mệnh đề:
A. Hãy cẩn thận!
B. X+Y=1
C. An hôm nay có phải đi học không?
D. An là học sinh giỏi
-
Câu 7:
Cho công thức logic mệnh đề: \(A = (p \to q) \wedge (\neg r \vee \neg q)\), hãy cho biết giá trị của A là gì?
A. 0
B. 1
C. Không xác định được
-
Câu 8:
Cho X là 1 biến Boole. Xác định biểu thức sai trong các biểu thức sau?
A. X.0=0
B. X.1=1
C. X+0=X
D. X+1=1
-
Câu 9:
Cho X là 1 biến Boole. Xác định biểu thức sai trong các biểu thức?
A. X+0=X
B. X+1=X
C. X + (Y + Z) = (X + Y) + Z = X + Y + Z
D. (W + X)(Y + Z) = WY + XY + WZ + XZ
-
Câu 10:
Hàm Boole f = x + xy tương đương với hàm nào sau đây?
A. f = xy
B. f = y
C. f = x+y
D. f = x
-
Câu 11:
Đại số Boole là…?
A. Một tập hợp với 2 phép toán cộng (+) và nhân (.)
B. Một tập hợp với các phép toán cộng (+) và nhân (.) và lấy phần bù.
C. Một tập hợp với các phép toán cộng (+) và nhân (.) và lấy phần bù; các phép cộng, nhân thoả các tính chất giao hoán, kết hợp, phân bố và có phần tử trung hoà.
D. Một tập hợp với các phép toán cộng (+) và nhân (.); các phép cộng, nhân thoả các tính chất giao hoán, kết hợp, phân bố và có phần tử trung hoà.
-
Câu 12:
Một đơn thức là?
A. Một tích khác không của một số hữu hạn các từ đơn (xi hoặc \(\overline {{x_i}} \))
B. Một tổng khác không của một số hữu hạn các từ đơn (xi hoặc ̅\(\overline {{x_i}} \))
C. Một tích khác không của đúng n từ đơn
D. Một tổng khác không của đúng n từ đơn
-
Câu 13:
Công thức đa thức là?
A. Công thức biểu diễn hàm Boole thành tích của các tích cơ bản (từ tối tiểu)
B. Công thức biểu diễn hàm Boole thành tổng của các tích cơ bản (từ tối tiểu)
C. Công thức biểu diễn hàm Boole thành tổng của các từ đơn
D. Công thức biểu diễn hàm Boole thành tổng của các đơn thức
-
Câu 14:
Dạng chính tắc tuyển (nối rời chính tắc) của hàm Boole là…?
A. Công thức biểu diễn hàm Boole thành tổng của các tích cơ bản (từ tối tiểu)
B. Công thức biểu diễn hàm Boole thành tích của các tích cơ bản (từ tối tiểu)
C. Công thức biểu diễn hàm Boole thành tổng của các đơn thức
-
Câu 15:
Trong bảng Karnaugh, 2 ô gọi là kề nhau nếu...?
A. Chúng nằm trên cùng 1 hàng
B. Chúng nằm trên cùng 1 cột
C. Nếu chúng cùng nằm trên 1 hàng, 1 cột hoặc chúng là ô đầu, ô cuối của cùng một hàng hoặc 1 cột nào đó
D. Nếu chúng là hai ô liền nhau hoặc chúng là ô đầu và ô cuối của cùng một hàng hoặc 1 cột nào đó
-
Câu 16:
Hãy cho biết có bao nhiêu tế báo tối đại trong bảng Karnaugh dươi đây?
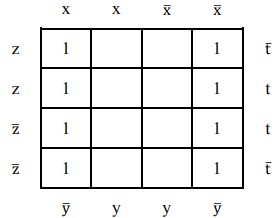
A. 3
B. 4
C. 5
D. 6
-
Câu 17:
Hãy cho biết có bao nhiêu tế báo tối đại trong bảng Karnaugh sau đây:
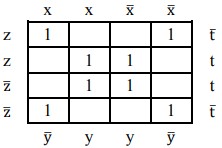
A. 1
B. 2
C. 3
D. 4
-
Câu 18:
Hãy cho biết có bao nhiêu tế báo tối đại trong bảng Karnaugh nào dưới đây?
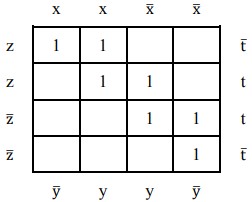
A. 3
B. 4
C. 5
D. 6
-
Câu 19:
Cho đồ thị vô hướng G=(V,E), với |V| = n; |E|=m. Tổng bậc của tất cả các đỉnh trong đồ thị G là?
A. -1.m
B. -2.m
C. 1.m
D. 2.m
-
Câu 20:
Cho đồ thị G có trọng số như hình sau:
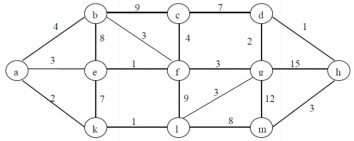
G là đồ thị có phải đồ thị Euler không? Vì sao?
A. Có vì các đỉnh của đồ thị đều có bậc chẵn
B. Không, vì nó chứa các đỉnh bậc lẻ (a,k,m,c,d,h)
C. Không, vì nó chứa các đỉnh bậc chẵn (a,k,m,c,d,h)
D. Có, vì nó chứa các đỉnh bậc chẵn (a,k,m,c,d,h)
-
Câu 21:
Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại trong đồ thị sau. Đỉnh E được gán trọng số nhỏ nhất là?
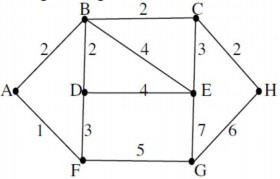
A. 3
B. 4
C. 5
D. 6
-
Câu 22:
Phát biểu nào dưới đây là đúng:
A. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
-
Câu 23:
Chọn phát biểu nào sau đây là đúng:
A. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh
-
Câu 24:
Phương án nào sau đây là đúng:
A. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh
-
Câu 25:
Cho G là đồ thị có hướng, phát biểu nào sau đây là chính xác nhất:
A. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.
B. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.
C. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.
D. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên
-
Câu 26:
Cho G là đồ thị có hướng, phát biểu nào sau đây là đúng nhất:
A. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.
B. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.
C. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.
D. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên
-
Câu 27:
Giả sử G=(V,E) là đồ thị vô hướng. Đỉnh x gọi là đỉnh cô lập nếu?
A. x có bậc 0
B. x có bậc 1
C. x có bậc 2
D. x có bậc 3
-
Câu 28:
Một đơn đồ thị vô hướng liên thông có 6 đỉnh, các đỉnh có bậc lần lượt là 2, 3, 3, 4, 2, 2. Tìm số cạnh của đồ thị?
A. 4
B. 6
C. 8
D. 10
-
Câu 29:
Có bao nhiêu cạnh trong đồ thị có 10 đỉnh, mỗi đỉnh có bậc là 6?
A. 0
B. 10
C. 20
D. 30
-
Câu 30:
Có bao nhiêu cạnh trong đồ thị có 10 đỉnh, mỗi đỉnh có bậc là 4?
A. 0
B. 10
C. 20
D. 30














