Trắc nghiệm Đường tiệm cận Toán Lớp 12
-
Câu 1:
Cho hàm số y = f(x) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\) và \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 1\)
Trong các khẳng định dưới đây, khẳng định nào là đúng?
-
Câu 2:
Cho các mệnh đề sau
(1) Đường thẳng y = y0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = {y_0} \vee \;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = {y_0}\)
(2) Đường thẳng y = y0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\; \vee \;\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\)
(3) Đường thẳng x = x0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = + \infty \; \vee \mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = - \infty \)
(4) Đường thẳng x = x0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = - \infty \; \vee \;\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x \right) = - \infty \)
-
Câu 3:
Cho hàm số \(y = \frac{{2x + \sqrt {{x^2} - 4} }}{{x - 2}}\) có đồ thị (C). Chọn mệnh đề đúng trong các mệnh đề sau:
-
Câu 4:
Tìm mệnh đề sai trong các mệnh đề sau:
-
Câu 5:
Cho hàm số bậc ba \(f(x)=a x^{3}+b x^{2}+c x+d\) có đồ thị như hình vẽ bên dưới:
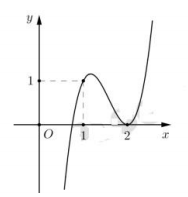
Hỏi đồ thị hàm số \(g(x)=\frac{\left(x^{2}-3 x+2\right) \sqrt{x-1}}{(x+1)\left[f^{2}(x)-f(x)\right]}\) có bao nhiêu đường tiệm cận đứng?
-
Câu 6:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình bên dưới:
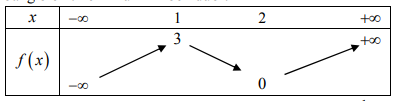
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2 f(x)-1}\) là
-
Câu 7:
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2 f(x)-1}\) là?
-
Câu 8:
Đồ thị hàm số \(y=\frac{5 x+1-\sqrt{x+1}}{x^{2}+2 x}\) có tất cả bao nhiêu đường tiệm cận?
-
Câu 9:
Cho hàm số \(y=\frac{5 \sqrt{x^{2}+6}+x-12}{4 x^{3}-3 x-1}\) có đồ thị (C) . Mệnh đề nào sau đây là đúng?
-
Câu 10:
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x-2}+1}{x^{2}-3 x+2}\) là:
-
Câu 11:
Hàm số \(y=\frac{x+\sqrt{x^{2}+x+1}}{x^{3}+x}\)có bao nhiêu đường tiệm cận?
-
Câu 12:
Cho hàm số \(y=\frac{x^{2}+2 x+3}{\sqrt{x^{4}-3 x^{2}+2}}\) Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
-
Câu 13:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x(4 x+6)}-2}{x+2}\)
-
Câu 14:
Đồ thị hàm số \(f(x)=\frac{x+1}{\sqrt{x^{2}-1}}\) có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
-
Câu 15:
Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+4}-2}{x^{2}+x}\) là?
-
Câu 16:
Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+16}-4}{x^{2}+x}\) là:
-
Câu 17:
Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+25}-5}{x^{2}+x}\)
-
Câu 18:
Tìm tất cả các tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x-1-\sqrt{x^{2}+x+3}}{x^{2}-5 x+6}\)
-
Câu 19:
Đồ thị hàm số \(y=\frac{x-2}{x^{2}-4}\) có mấy tiệm cận?
-
Câu 20:
Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+9}-3}{x^{2}+x}\)
-
Câu 21:
Tìm số tiệm cận đứng của đồ thị hàm số \(y=\frac{x^{2}-3 x-4}{x^{2}-16}\).
-
Câu 22:
Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+4}-2}{x^{2}+x}\) là:
-
Câu 23:
Tìm số tiệm cận của đồ thị hàm số \(y=\frac{x^{2}-5 x+4}{x^{2}-1}\)
-
Câu 24:
Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
-
Câu 25:
Cho hàm số \(y = f(x)\, {\rm{ có }}\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x) = - 1\). Khẳng định nào sau đây là khẳng định đúng?
-
Câu 26:
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x+1}{x+1} ?\)
-
Câu 27:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R} \backslash\{1\}\) có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y=f(x).
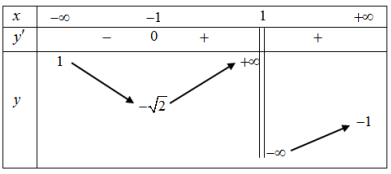
-
Câu 28:
Cho hàm số có bảng biến thiên như hình sau:

Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y=f(x) là -
Câu 29:
Cho hàm số y=f(x) có bảng biến thiên như sau:
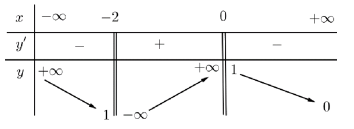
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng -
Câu 30:
Cho hàm số y=f(x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: -
Câu 31:
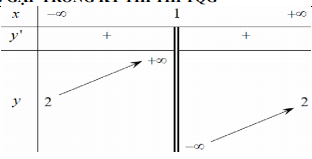
Cho hàm số y=f(x) có bảng biến thiên như sau
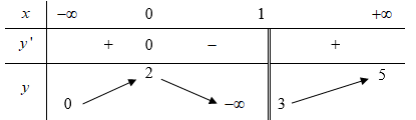
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: -
Câu 32:
Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là đúng?
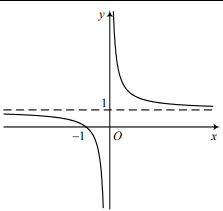
-
Câu 33:
Cho hàm số y=f(x) có bảng biến thiên như sau
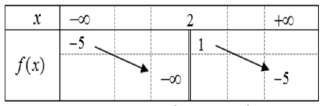
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: -
Câu 34:
Cho hàm số y=f(x) có bảng biến thiên như sau:
.png)
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: -
Câu 35:
Cho hàm số y=f(x) có bảng biến thiên như sau:
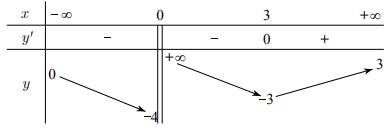
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là? -
Câu 36:
Cho hàm số bậc ba \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iaadggacaWG4bWaaWba % aSqabeaacaaIZaaaaOGaey4kaSIaamOyaiaadIhadaahaaWcbeqaai % aaikdaaaGccqGHRaWkcaWGJbGaamiEaiabgUcaRiaadsgaaaa!458D! f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaWaaeWaaeaa % caWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaG4maiaadIhacq % GHRaWkcaaIYaaacaGLOaGaayzkaaWaaOaaaeaacaaIYaGaamiEaiab % gUcaRiaaigdaaSqabaaakeaadaqadaqaaiaadIhadaahaaWcbeqaai % aaisdaaaGccqGHsislcaaI1aGaamiEamaaCaaaleqabaGaaGOmaaaa % kiabgUcaRiaaisdaaiaawIcacaGLPaaacaGGUaGaamOzamaabmaaba % GaamiEaaGaayjkaiaawMcaaaaaaaa!528F! g\left( x \right) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} - 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
.png)
-
Câu 37:
Cho hàm số y = f(x) xác định trên R\{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
.png)
-
Câu 38:
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaWaaOaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGa % eyOeI0IaaGinaaWcbeaaaOqaaiaadIhadaahaaWcbeqaaiaaikdaaa % GccqGHsislcaaI1aGaamiEaiabgUcaRiaaiAdaaaaaaa!4202! y = \frac{{\sqrt {{x^2} - 4} }}{{{x^2} - 5x + 6}}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang ?
-
Câu 39:
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9 % Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWG5bGaeyypa0 % ZaaSaaaeaacaWG4bGaey4kaSIaaGymaaqaaiaadIhacqGHsislcaaI % Yaaaaaaa!3CD5! y = \frac{{x + 1}}{{x - 2}} (C)\) có các đường tiệm cận là
-
Câu 40:
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iaadIhadaahaaWcbeqa % aiaaikdaaaGccqGHsislcaWG4bGaeyOeI0IaciiBaiaac6gacaWG4b % aaaa!4212! f\left( x \right) = {x^2} - x - \ln x\). Biết trên đoạn [1;e] hàm số có GTNN là m, và có GTLN là M . Hỏi M + m bằng:
-
Câu 41:
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gkHiTiaaigdaaaaaaa!3E03! y = \frac{{2x + 1}}{{x - 1}}\). Đường tiệm cận đứng của đồ thị hàm số là:
-
Câu 42:
Cho hàm số y =f(x) có bảng biến thiên:
Đồ thị hàm số có tiệm cận đứng là đường thẳng có phương trình là
.png)
-
Câu 43:
Gọi (C) là đồ thị của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHsislcaaI0aaabaGaamiEaiab % gkHiTiaaiodaaaaaaa!3E12! y = \frac{{2x - 4}}{{x - 3}}\). Trong các mệnh đề sau, tìm mệnh đề sai.
-
Câu 44:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiaadIhacqGHRaWkcaaIYaaabaGaamiEaiab % gUcaRiaaigdaaaaaaa!3DFA! y = \frac{{3x + 2}}{{x + 1}}\).
-
Câu 45:
Đường thẳng y =2 là tiệm cận ngang của đồ thị nào dưới đây?
-
Câu 46:
Phương trình đường tiệm cận ngang của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiabgkHiTiaaisdacaWG4baabaGaeyOeI0Ia % aGOmaiaadIhacqGHRaWkcaaIXaaaaaaa!3FB0! y = \frac{{3 - 4x}}{{ - 2x + 1}}\) là:
-
Câu 47:
Cho hàm số y = f(x) có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcaaIXaWaaWbaaWqa % beaacqGHRaWkaaaaleqaaOGaamOzamaabmaabaGaamiEaaGaayjkai % aawMcaaiabg2da9iabgUcaRiabg6HiLcaa!4491! \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcaaIXaWaaWbaaWqa % beaacqGHsislaaaaleqaaOGaamOzamaabmaabaGaamiEaaGaayjkai % aawMcaaiabg2da9iaaikdaaaa!4305! \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 2\). Mệnh đề nào sau đây đúng?
-
Câu 48:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
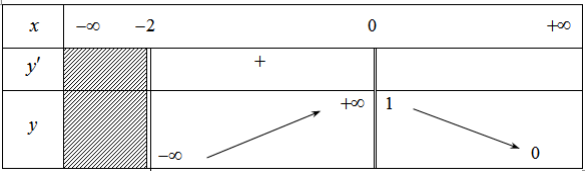
-
Câu 49:
Cho hàm số y=f(x) có bảng biến thiên như sau
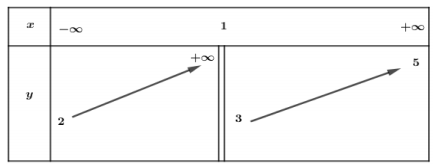
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là -
Câu 50:
Cho hàm số y=f(x) có bảng biến thiên như sau:
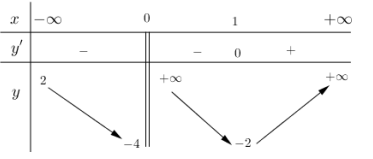
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:











