Trắc nghiệm Đường tiệm cận Toán Lớp 12

Câu 1:

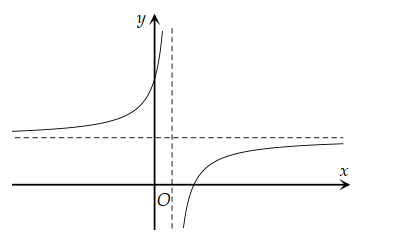
Cho hàm số \(y=\frac{a x+b}{c x+d} \text { có }\) có đồ thị như hình vẽ bên dưới:

Khẳng định nào sau đây sai?

Câu 2:

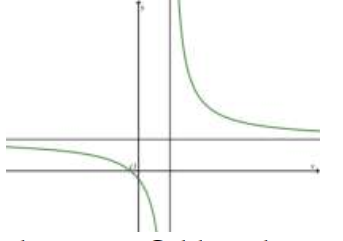
Đường cong ở hình bên là đồ thị của hàm số \(y=\frac{a x+b}{c x+d} \text { với } a, b, c, d\)  là các số thực. Khẳng định nào dưới đây đúng 

Câu 3:

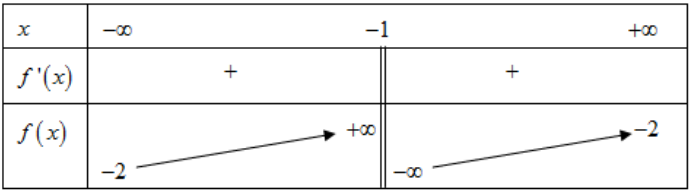
Cho hàm số \(y=\frac{a x+b}{c x+d} ;(a, b, c, d \in \mathbb{R}) \) có bảng biến thiên như sau: 

Khẳng định nào dưới đây đúng?
 

Câu 4:

Cho hàm số \(f(x)=\frac{a x+1}{b x+c}(a, b, c \in \mathbb{R})\)có bảng biến thiên như sau: 

Trong các số a b , và c có bao nhiêu số dương?

Câu 5:

Cho hàm số \(y=\frac{a x+1}{b x-2},(a ; b \in \mathbb{R}),\) có đồ thị như hình vẽ sau:

\(\text { Tính } T=a+b \text { . }\)

Câu 6:

Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số \(y=\frac{5 x-3}{x^{2}-2 m x+1}\) không có tiệm cận
đứng. 

Câu 7:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017; 2017] để hàm số \(y=\frac{x+2}{\sqrt{x^{2}-4 x+m}}\) có hai tiệm cận đứng? 

Câu 8:

Có bao nhiêu giá trị m để đồ thị hàm số \(y=\frac{m x^{2}-1}{x^{2}-3 x+2}\) có đúng hai đường tiệm cận? 

Câu 9:

Tập hợp các giá trị của m để đồ thị hàm số \(y=\frac{x^{2}}{x^{3}-m}\) có tiệm cận đứng là 

Câu 10:

Tập hợp các giá trị của m để đồ thị hàm số \(y=\frac{x^{2}}{x-m}\) có tiệm cận đứng là 

Câu 11:

Cho hàm số \(y=\frac{x-1}{x+m}(m \neq-1)\) có đồ thị là (C) . Tìm để đồ thị (C) nhận điểm I(2;1) làm tâm đối xứng.

Câu 12:

Biết rằng đồ thị của hàm số \(y=\frac{(n-3) x+n-2017}{x+m+3}\)( m n , là các số thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m+n . 

Câu 13:

Tìm tham số m để đồ thị hàm số \(y=\frac{(m+1) x-5 m}{2 x-m}\) có tiệm cận ngang là đường thẳng y=1 .

Câu 14:

Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y=\frac{x+1}{x+m}\) có đường tiệm cận đứng là x=-1 là 

Câu 15:

Tập hợp tất cả các giá trị của tham số để đồ thị hàm số \(y=\frac{x-1}{x^{2}+2 m x+m}\)có ba đường tiệm cận là?

Câu 16:

Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y=\frac{x+1}{x^{2}+m}\) có ba đường tiệm cận là:

Câu 17:

Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y=\frac{m x+1}{x+1}\) có hai đường tiệm cận là:
 

Câu 18:

Đồ thị hàm số \(y=\frac{\sqrt{1-x^{2}}}{x-2}\) có số đường tiệm cận đứng là 

Câu 19:

Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số \(y=\frac{2 \sqrt{x^{2}-1}+1}{x}\) là?

Câu 20:

Số tiệm cận (đứng và ngang) của đồ thị hàm số \(y=\frac{x+1}{\sqrt{x^{3}-1}}\) là?

Câu 21:

Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 

Câu 22:

Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x-1}+1}{x^{2}-3 x}\) là?

Câu 23:

Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x-2}+1}{x^{2}-3 x+2}\) là?

Câu 24:

Tìm số đường tiệm cận của đồ thị hàm số \(y=\frac{x-1}{4 \sqrt{3 x+1}-3 x-5}\)

Câu 25:

Tìm tất cả các tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x-1-\sqrt{x^{2}+x+3}}{x^{2}-5 x+6}\)

Câu 26:

Đồ thị hàm số \(y=\frac{\sqrt{4-x^{2}}}{x^{2}-3 x-4}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang ? 

Câu 27:

Đồ thị hàm số \(y=\frac{\sqrt{x^{2}-4}}{x^{2}-5 x+6}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? 

Câu 28:

Đồ thị hàm số \(y=\frac{x^{2}+3}{x^{2}-2|x|-3}\) có tổng số tiệm cận đứng và tiệm cận ngang là?

Câu 29:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{2-x}{1+|x|} \mid\) là?

Câu 30:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x-1}{|x|-1}\) là?

Câu 31:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{x^{3}-x^{2}-x+1}\) là?

Câu 32:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{\sqrt{x-1}}{x^{2}-1}\) là?

Câu 33:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{\sqrt{x}}{x^{2}-1}\) là?

Câu 34:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x+1}{x^{2}-1}\) là?

Câu 35:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{2 x-1}{x^{2}-1}\) là?

Câu 36:

Tổng số các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{x^{3}-2 x^{2}}\) là?

Câu 37:

Đồ thị của hàm số \(y=\frac{x-1}{x^{2}+2 x-3}\) có bao nhiêu đường tiệm cận?

Câu 38:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x+3}{x-1}\)

Câu 39:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{x^{2}-4}\) là:

Câu 40:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{x}{x^{2}-1}\)nằm bên phải trục tung là 

Câu 41:

Tìm số tiệm cận đứng của đồ thị hàm số \(y=\frac{x^{2}-3 x-4}{x^{2}-16}\)

Câu 42:

Đồ thị hàm số \(y=\frac{-3 x+1}{x+2}\) có các đường tiệm cận đứng, tiệm cận ngang lần lượt là 

Câu 43:

Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào dưới đây? 

Câu 44:

Đồ thị hàm số \(y=\frac{x+1}{4 x-1}\) có đường tiệm cận ngang là đường thẳng nào dưới đây? 

Câu 45:

Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? 

Câu 46:

Số đường tiệm cận của đồ thị hàm số \(y=\frac{2}{x-9}\) là

Câu 47:

Tâm đối xứng của đồ thị hàm số \(y=\frac{2 x+1}{x-1}\) có tọa độ là

Câu 48:

Trong các hàm số sau, đồ thị hàm số nào có nhiều tiệm cận nhất? 

Câu 49:

Đồ thị hàm số nào sau đây có nhiều đường tiệm cận nhất?

Câu 50:

Đồ thị hàm số nào sau đây không có tiệm cận ngang?