Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12

Câu 1:

Hàm số y = 2x³-9x²+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình \(2{\left| x \right|^3} - 9{x^{2\;}}\; + \;12\left| x \right|\; + \;m\; = \;0\) có sáu nghiệm phân biệt.

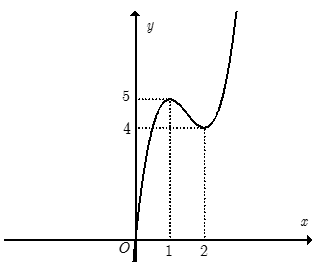
Câu 2:

Cho hàm số y = f(x) có đạo hàm trên R thoả f( 2) = f( -2) = 0 và đồ thị của hàm số y = f’ (x) có dạng như hình bên. Hàm số y = (f( x)) ² nghịch biến trên khoảng nào trong các khoảng sau ?

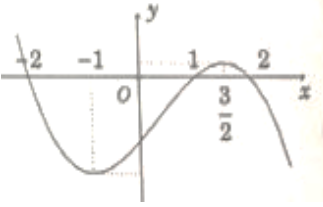
Câu 3:

Cho hàm số y = f(x). Biết f(x) có đạo hàm f’(x) và hàm số y = f’(x) có đồ thị như hình vẽ. Đặt g(x) = f(x+1). Kết luận nào sau đây đúng?

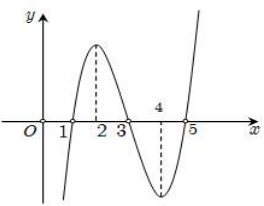
Câu 4:

Bất phương trình \(\sqrt {{x^2} - 2x + 3}  - \sqrt {{x^2} - 6x + 11}  > \sqrt {3 - x}  - \sqrt {x - 1} \) có tập nghiệm (a; b]. Hỏi hiệu b-a có giá trị là bao nhiêu?

Câu 5:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2}  = 2x + 1\) có hai nghiệm thực?

Câu 6:

Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x²-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx²+(m+1) x+m+1 ≥ 0.

Câu 7:

Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số \(y = \ln \left( {{x^2} + 1} \right) - mx + 1\) đồng biến trên khoảng ( -∞; +∞).

Câu 8:

Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y = f(x) = 2x+a.sinx+b.cosx luôn tăng trên R?

Câu 9:

Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số sau luôn giảm trên R?

\(y = f\left( x \right) = \frac{{ - {x^3}}}{3} + \frac{1}{2}\left( {\sin \alpha  + \cos \alpha } \right){x^2} - \frac{3}{2}x\sin \alpha \cos \alpha  - \sqrt {\beta  - 2} \)

Câu 10:

Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số \(y = \frac{{2{x^2} + \left( {1 - m} \right)x + 1 + m}}{{x - m}}\) đồng biến trên khoảng (1;+∞)?

Câu 11:

Có bao nhiêu giá trị nguyên dương của m để hàm số y = 3x+ m(sinx+ cosx+m) đồng biến trên R ?

Câu 12:

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = {x^3} + mx - \frac{1}{{5{x^5}}}\) đồng biến với x > 0?

Câu 13:

Hỏi phương trình 3x²- 6x+ ln( x+1) 3+1 = 0 có bao nhiêu nghiệm phân biệt?

Câu 14:

Cho phương trình x³- 3x²+ 1- m = 0  (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa mãn x₁ < 1< x₂ < x₃ khi

Câu 15:

Tìm tập hợp tất cả các giá trị của tham số thực của m để hàm số y = ln( x²+ 1) –mx+1 đồng biến trên R.

Câu 16:

Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} + \left( {4 - m} \right)\frac{{{x^2}}}{2} + \left( {5 - 2m} \right)x + {m^2} + 3,\), với m là tham số thực. 
 Hàm số \(g\left( x \right) = \frac{{{x^2} + 4x + 5}}{{x + 2}}\) có đồ thị C và bảng biến thiên sau:

Tìm m sao cho hàm số f(x)  đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1

Câu 17:

Với giá trị nào của tham số m thì hàm số \(y = \sin \left( x \right) - \cos \left( x \right) + 2017\sqrt 2 mx\) đồng biến trên R.

Câu 18:

Cho hàm số y = f( x)  có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 9} \right){\left( {x - 4} \right)^2}.\).  Xét hàm số y = g( x) = f(x²) 

Trong các phát biểu sau; tìm số phát biểu đúng

I. Hàm số y = g( x) đồng biến trên( 3; +∞)

II. Hàm số y = g(x) nghịch biến trên( -∞; -3)

III. Hàm số y = g( x) có 5 điểm cực trị

IV. \(\mathop {min}\limits_{x \in R} \;g\left( x \right) = f\left( 9 \right)\)

Câu 19:

Cho hàm số y = f( x).(x-1) liên tục trên R và có đồ thị như hình vẽ.

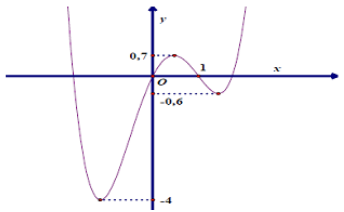
Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x - 1| = m có số nghiệm lớn nhất

Câu 20:

Cho hàm số y = f(x) = x⁴+ 2mx²+ m. Tìm m để f(x) > 0 với mọi m.

Câu 21:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3\sqrt {x - 1}  + m\sqrt {x + 1}  = 2\sqrt[4]{{{x^2} - 1}}\) có hai nghiệm thực?

Câu 22:

Tìm tất cả các giá trị thực của tham số m  sao cho phương trình \(\sqrt {{x^2} + mx + 2}  = 2x + 1\) có hai nghiệm thực?

Câu 23:

Bất phương trình \(\sqrt {{x^2} - 2x + 3}  - \sqrt {{x^2} - 6x + 11}  > \sqrt {3 - x}  - \sqrt {x - 1} \) có tập nghiệm là ( a; b]. Hỏi 4a-b có giá trị là bao nhiêu?

Câu 24:

Tập nghiệm của bất phương trình: \(\sqrt {5x - 1}  + \sqrt {x + 3}  \ge 4\) có bao nhiêu giá trị nguyên trong ( 0; 2008]

Câu 25:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{\tan \;x - 2}}{{\tan \;x\; - \;m}}\) đồng biến trên khoảng \(\left( {0;\frac{{\rm{\pi }}}{4}} \right)\)?

Câu 26:

Cho phương trình: \(2{x^3} + {x^2} - 3x + 1 = 2\left( {3x - 1} \right)\sqrt {3x - 1} \)

Tính tổng các nghiệm cùa phương trình là :

Câu 27:

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

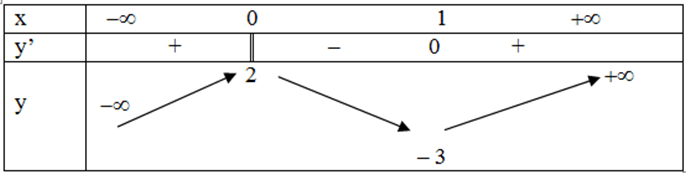
Khẳng định nào sau đây là khẳng định đúng?

Câu 28:

Cho hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 3\). Khẳng định nào sau đây đúng?

Câu 29:

Hàm số y = x³ – 3x đồng biến trên khoảng nào?

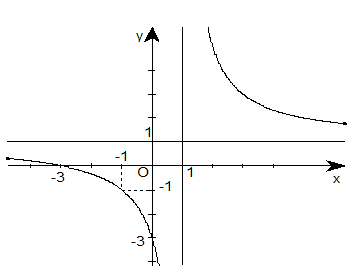
Câu 30:

Đường cong hình bên là đồ thị của một hàm số. Hãy chọn khẳng định đúng

Câu 31:

Cho hàm số y = f(x) có đồ thị như hình vẽ.

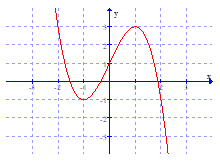
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?

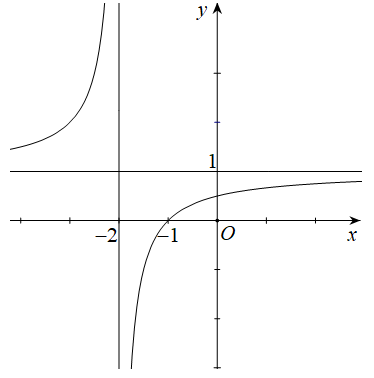
Câu 32:

Hàm số y = f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?

Câu 33:

Cho hàm số y = x⁴ – 2x² + 2. Kết luận nào sau đây sai?

Câu 34:

Cho hàm số y = - x³ + 3x² – 3x + 7. Mệnh đề nào sau đây là đúng?

Câu 35:

Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{{x^2}}}{2} - 6x + \frac{3}{4}\). Chọn khẳng định đúng.

Câu 36:

Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) là đúng?

Câu 37:

Hàm số y = 2x² – x⁴ nghịch biến trên những khoảng nào?

Câu 38:

Cho hàm số \(y = \frac{{ - x + 5}}{{x + 2}}\). Mệnh đề nào sau đây là đúng?

Câu 39:

Tìm khoảng nghịch biến của hàm số y = 2x³ – 9x² + 12x + 4

Câu 40:

Các khoảng đồng biến của hàm số y = - x³ + 3x² + 1 là

Câu 41:

Cho hàm số y = - x⁴ + 2x². Hỏi hàm số đã cho đồng biến trên khoảng nào sau đây?

Câu 42:

Hàm số y = x³ – 3x² – 9x + 1 đồng biến trên mỗi khoảng:

Câu 43:

Cho hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 3\). Khẳng định nào sau đây đúng?

Câu 44:

Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\). Tìm mệnh đề đúng

Câu 45:

Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định của chúng?

Câu 46:

Cho hàm số y = x⁴ – 2x² + 3. Tìm các khoảng đồng biến của hàm số

Câu 47:

Hàm số y = x³ – 3x đồng biến trên khoảng nào?

Câu 48:

Hàm số \(y =  - {x^3} + 3{x^2} + 2\) đồng biến trên khoảng nào?

Câu 49:

Hỏi hàm số \(y =  - \frac{1}{3}{x^3} + 2{x^2} + 5x - 44\) đồng biến trên khoảng nào?

Câu 50:

Hàm số y = x³ – 3x² + 2 đồng biến trên khoảng nào trong các khoảng cho dưới đây