Trắc nghiệm Hàm số lượng giác Toán Lớp 11
-
Câu 1:
Tìm chu kì của các hàm số sau \( y = \tan x + \tan \frac{x}{2}\)
-
Câu 2:
Tìm chu kì của các hàm số sau y = tan x.tan 3x
-
Câu 3:
Tìm giá trị nhỏ nhất của hàm số \(y = tan ^2x - 4tan x + 1 \)
-
Câu 4:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2sin ^2x + cos ^22x\)
-
Câu 5:
Tìm chu kì cơ sở (nếu có) của các hàm số sau \(y = sin 3x + 2cos 2x \)
-
Câu 6:
Tìm tập xác định của hàm số \( y = \sqrt {\frac{{1 - \cos 3x}}{{1 + \sin 4x}}} \)
-
Câu 7:
Tìm chu kì của các hàm số sau \(f( x ) = sin 2x + sin x \)
-
Câu 8:
Tìm tập xác định của hàm số sau \(y= \tan \left( {2x + \frac{\pi }{3}} \right)\)
-
Câu 9:
Tìm tập xác định của hàm số \(y= \tan \left( {2x - \frac{\pi }{4}} \right)\)
-
Câu 10:
Tìm tập xác định của hàm số sau \(y = tan 3x.cot 5x\)
-
Câu 11:
Hàm số \( y = \frac{{1 - 2\sin x}}{{\cos 3x - 1}}\) xác định trên:
-
Câu 12:
Tìm chu kì của các hàm số sau \( f\left( x \right) = \sin \left( {x + \frac{\pi }{5}} \right)\)
-
Câu 13:
Tìm chu kì của hàm số y = f( x ) = tan 2x
-
Câu 14:
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \( \frac{3}{{1 + \sqrt {2 + {{\sin }^2}x} }}\)
-
Câu 15:
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \( {\frac{4}{{1 + 2{{\sin }^2}x}}}\)
-
Câu 16:
Đồ thị hàm số y = tan x nhận đường thẳng nào sau đây là tiệm cận?
-
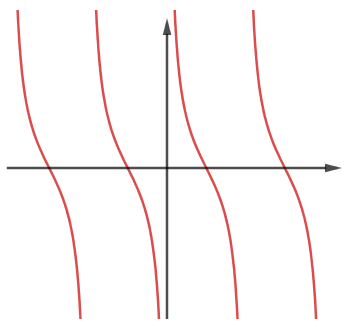
Câu 17:
Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây?
-
Câu 18:
Chọn mệnh đề đúng:
-
Câu 19:
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = 3 - 2cos ^2 3x \)
-
Câu 20:
Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau \( y = 1 + 3\sin \left( {2x - \frac{\pi }{4}} \right)\)
-
Câu 21:
Trong các hàm số sau đây là hàm số lẻ
-
Câu 22:
Hàm số nào dưới đây là hàm số chẵn?
-
Câu 23:
Hàm số nào sau đây không là hàm số lẻ?
-
Câu 24:
Điểm O (0;0) luôn thuộc đồ thị hàm số
-
Câu 25:
Đồ thị hàm số y = tan x luôn đi qua điểm nào dưới đây?
-
Câu 26:
Hàm số y = sin x nghịch biến trên khoảng nào dưới đây:
-
Câu 27:
Hàm số y = cos x nghịch biến trên mỗi khoảng:
-
Câu 28:
Hàm số nào sau đây có tập giá trị là R?
-
Câu 29:
Tập giá trị của hàm số y = sin x là:
-
Câu 30:
Tập xác định của hàm số y = 2sin x là
-
Câu 31:
Hàm số y = cos x xác định trên:
-
Câu 32:
Hàm số y = sin x có tập xác định là
-
Câu 33:
Tìm điều kiện xác định của hàm số \(y=\frac{1-3 \cos x}{\sin x}\)
-
Câu 34:
Tìm tập xác định D của hàm số \(y=\cot x+\sin 5 x+\cos x\)
-
Câu 35:
Hàm số \(y=\frac{2 \sin x+1}{1-\cos x}\)xác định khi
-
Câu 36:
Cho \(x, y, z>0 \text { và } x+y+z=\frac{\pi}{2}\)Tìm giá trị lớn nhất của \(y=\sqrt{1+\tan x \cdot \tan y}+\sqrt{1+\tan y \cdot \tan z}+\sqrt{1+\tan z \cdot \tan x}\)
-
Câu 37:
Cho hàm số \(y=\frac{1}{2-\cos x}+\frac{1}{1+\cos x} \text { vói } x \in\left(0 ; \frac{\pi}{2}\right)\) Kết luận nào sau đây là đúng?
-
Câu 38:
Tìm giá trị lớn nhất của hàm số \(y=\sqrt{1+\frac{1}{2} \cos ^{2} x}+\frac{1}{2} \sqrt{5+2 \sin ^{2} x}\).
-
Câu 39:
Giá trị nhỏ nhất của hàm số \(y=\sin x \sqrt{\cos x}+\cos x \sqrt{\sin x}\) là:
-
Câu 40:
Giá trị lớn nhất của hàm số \(y=\sin ^{4} x+\cos ^{4} x+\sin x \cos x\) là:
-
Câu 41:
Hàm số \(y=2 \cos x+\sin \left(x+\frac{\pi}{4}\right)\) đạt giá trị lớn nhất là
-
Câu 42:
Hàm số \(y=4 \cot ^{2} 2 x-\frac{\sqrt{3}\left(1-\tan ^{2} x\right)}{\tan x}\) đạt giá trị nhỏ nhất là
-
Câu 43:
Tìm tập xác định D của hàm số \(y=\sqrt{5+2 \cot ^{2} x-\sin x}+\cot \left(\frac{\pi}{2}+x\right)\)
-
Câu 44:
Hàm số \(y=\tan x+\cot x+\frac{1}{\sin x}+\frac{1}{\cos x}\) không xác định trong khoảng nào trong các khoảng sau đây?
-
Câu 45:
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y=\frac{\sin x+\cos x}{2 \sin x-\cos x+3}\) lần lượt là:
-
Câu 46:
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y=3(3 \sin x+4 \cos x)^{2}+4(3 \sin x+4 \cos x)+1\)
-
Câu 47:
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y=\frac{\sin ^{2} 2 x+3 \sin 4 x}{2 \cos ^{2} 2 x-\sin 4 x+2}\)
-
Câu 48:
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y=3 \cos x+\sin x-2\)
-
Câu 49:
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y=\frac{2 \sin ^{2} 3 x+4 \sin 3 x \cos 3 x+1}{\sin 6 x+4 \cos 6 x+10}\)
-
Câu 50:
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y=\frac{\sin 2 x+2 \cos 2 x+3}{2 \sin 2 x-\cos 2 x+4}\)